Giải bởi Vietjack
Lời giải
Đáp án đúng là: D
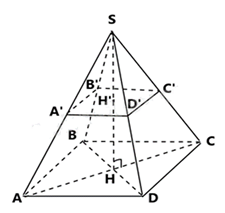
\[SH = 4\,\,m\] là chiều cao của bugalow
\[ \Rightarrow SH' = \frac{{SH}}{2} = 2\,\,(m)\]
\[A'B' = \frac{1}{2}AB = \frac{1}{2}.\,6 = 3\,\,(m)\]
Ta có:
\[{S_{A'B'C'D'}} = 3\,.\,3 = 9\,\,\left( {{m^2}} \right)\]
\[{{\rm{S}}_{{\rm{ABCD}}}}{\rm{ = 6}}{\rm{.6 = 36}}{{\rm{m}}^{\rm{2}}}\]
\[{V_{S.A'B'C'D'}} = \frac{1}{3}.{S_{A'B'C'D'}}\,.\,SH' = \frac{1}{3}.\,9\,.\,2{\rm{ }} = 6\,\,\left( {{m^3}} \right)\]
\[{V_{S.ABCD}} = \frac{1}{3}.\,{S_{ABCD}}\,.\,SH = \frac{1}{3}.\,36\,.\,4 = 48\,\,\left( {{m^3}} \right)\]
Thể tích phần không gian còn lại ở tầng dưới là:
\[{\rm{V = }}{{\rm{V}}_{{\rm{S}}{\rm{.ABCD}}}} - {{\rm{V}}_{{\rm{S}}{\rm{.A'B'C'D'}}}}{\rm{ = 48}} - 6 = 42\,\,\left( {{m^3}} \right)\]
