Cho A = 2 + 22 + 23 + ... + 220. Chứng minh rằng:
a) A chia hết cho 2;
b) A chia hết cho 3;
c) A chia hết cho 5.
Giải bởi Vietjack
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:
A = 2 + 22 + 23 + ... + 220
A = (2 + 22) + (23 + 24) + ... + (219 + 220)
A = 2(1 + 2) + 23(1 + 2) +… + 219(1 + 2)
A = 3.(2 + 23 + … + 219)
Từ đó A chia hết cho 3
c) Tương tự câu b ta có:
A = 2 + 22 + 23 + ... + 220
A = (2 + 23) + (22 + 24) + ... + (218 + 220)
A = 5.(2 + 22 + 25 … + 218)
Từ đó A chia hết cho 5.
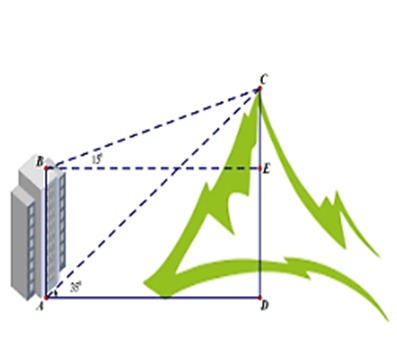
Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao 60 m.
Cho tam giác ABC vuông tại A, AC = b, AB = c. Lấy điểm M trên cạnh BC sao cho \(\widehat {BAM} = 30^\circ \).Tính tỉ số \(\frac{{MB}}{{MC}}\).
Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1, 2, 3.
Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m, chiều rộng 5m, chiều sâu 3m.
a) Tính thể tích của hồ bơi.
b) Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).
c) Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.
Cho hình vuông ABCD. Trên cạnh các AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Gọi M, N lần lượt là trung điểm của EF, BF.
a) Chứng minh các tam giác ADF và BAE bằng nhau.
b) Chứng minh MN vuông góc AF.
Bác Ngọc thực hiện chế độ ăn kiêng với yêu cầu tối thiểu hằng ngày qua thức uống là 300 ca – lo, 36 đơn vị vitamin A và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca – lo, 12 đơn vị vitamin A và 10 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ hai cung cấp 60 ca – lo, 6 đơn vị vitamin A và 30 đơn vị vitamin C.
a) Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca – lo và số đơn vị vitamin hấp thụ.
b) Chỉ ra hai phương án mà bác Ngọc có thể chọn lựa số lượng cốc cho đồ uống thứ nhất và thứ hai nhằm đáp ứng nhu cầu cần thiết đối với số ca – lo và số đơn vị vitamin hấp thụ.
Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tích vô hướng của hai vectơ \(\overrightarrow {BC} .\overrightarrow {CG} \)
Một trường trung học phổ thông có 4 học sinh giỏi khối 12, có 5 học sinh giỏi khối 11, có 6 học sinh giỏi khối 10. Hỏi có bao nhiêu cách sắp xếp 15 học sinh trên thành một hàng ngang để đón đoàn đại biểu, nếu các học sinh ở cùng một khối thì xếp gần nhau.
Cho tam giác ABC có AB = 6cm, AC = 8cm. Gọi H là chân đường vuông góc kẻ từ B đến tia phân giác của Â, M là trung điểm của BC. Tính HM?
Giả sử ta dùng thước và compa vẽ hình thoi ABCD, biết AB = 5cm và AC = 8cm.
Cho nửa đường tròn (O; R) đường kính AB, vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Trên tia Ax lấy điểm E (E khác A, AE < R), trên nửa đường tròn lấy điểm M sao cho EM = EA, đường thẳng Em cắt tia By tại F.
a) Chứng minh EF là tiếp tuyến của đường tròn (O).
b) Chứng minh tam giác EOF là tam giác vuông.
c) Chứng minh AM.OE + BM.OF = AB.EF.
Cho hình thang cân ABCD có đáy lớn CD = 3, đáy nhỏ AB = 1 và AD = BC = \(\sqrt 5 \), gọi I là giao điểm của hai đường chéo hình thang, gọi H là trực tâm của tam giác BDC. Phân tích vectơ \(\overrightarrow {IH} \) theo vectơ \(\overrightarrow {AB} ,\overrightarrow {AD} \).
Có bao nhiêu số tự nhiên có ba chữ số phân biệt sao cho tổng các chữ số là lẻ?
Một trang trại nuôi ong mật mua 75 chiếc can loại 10 lít để đựng mật ong chuẩn bị cho vụ thu hoạch vào vụ thu hoạc số mật ong tăng gấp đôi so với dự kiến vậy để đựng hết số mật ong thu hoạch được trại nuôi ong cần mấy can 10 lít.
