Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 4, \[\widehat {BAC} = 30^\circ \]. Mặt phẳng (P) song song với (ABC) cắt đoạn SA tại M sao cho SM = 2MA. Diện tích thiết diện của (P) và hình chóp S.ABC bằng bao nhiêu?
A. \(\frac{{16}}{9}.\)
B. \(\frac{{14}}{9}.\)
C. \(\frac{{25}}{9}.\)
D. 1.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
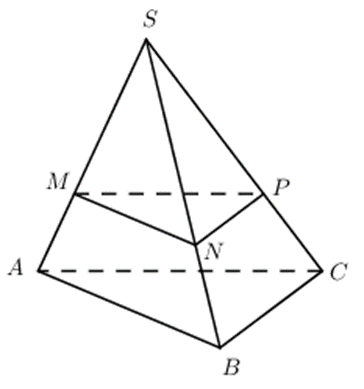
Trong ( SAB ) qua M kẻ MN // AB, trong (SAC) kẻ MP // AC.
Khi đó ta có (MNP) // (ABC).
\( \Rightarrow \left( {MNP} \right) \equiv \left( P \right){\rm{.\;}}\)
Thiết diện của (P) và hình chóp là tam giác MNP đồng dạng với tam giác ABC theo tỉ số: \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\)
\( \Rightarrow \frac{{{S_{MNP}}}}{{{S_{ABC}}}} = {\left( {\frac{2}{3}} \right)^2} = \frac{4}{9} \Rightarrow {S_{MNP}} = \frac{4}{9}{S_{ABC}}\)
Ta có \({S_{ABC}} = \frac{1}{2}AB \cdot AC \cdot {\rm{sin}}\widehat {BAC} = \frac{1}{2} \cdot 4 \cdot 4 \cdot {\rm{sin}}30^\circ = 4\)
\( \Rightarrow {S_{MNP}} = \frac{4}{9} \cdot 4 = \frac{{16}}{9}\)
Đáp án cần chọn là: \({\rm{A}}\)
Cho hình bình hành ABCD, I là giao điểm hai đường chéo. Khi đó, khẳng định nào sau đây là đúng?
Cho phương trình \({\rm{cot}}x = \sqrt 3 .\) Các nghiệm của phương trình là:
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng a và b có phương trình lần lượt là 4x + 3y + 5 = 0 và x + 7y ‒ 4 = 0. Nếu có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay φ (0 ≤ φ ≤ 180°) là:
Trong mặt phẳng Oxy cho đường thẳng (d: 2x ‒ y + 1 = 0 ). Để phép quay tâm I góc quay (2017π) biến d thành chính nó thì tọa độ của I là:
Xét phép vị tự V(I,3) biến tam giác ABC thành tam giác A'B'C'. Hỏi chu vi tam giác A'B'C' gấp mấy lần chu vi tam giác ABC.
Biết \[\sin a + \cos a = \sqrt 2 \]. Hỏi giá trị của sin4a + cos4a bằng bao nhiêu ?
Cho tam giác ABC. Gọi M là điểm được xác định: \(4\overrightarrow {BM} - 3\overrightarrow {BC} = \vec 0\). Khi đó vectơ \(\overrightarrow {AM} \) bằng
Cho tam giác ABC có trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây đúng?
Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng \[\frac{a}{6}\]Thể tích khối lăng trụ bằng
Mệnh đề nào đúng?
Cho hai đường thẳng d1 và d2 song song có bao nhiêu phép tịnh tiến biến đường thẳng d1 thành đường thẳng d2:
Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ \[\overrightarrow {OC} \] có điểm đầu và điểm cuối là các đỉnh của lục giác là:
Số mặt phẳng đối xứng của hình hộp chữ nhật (các kích thước khác nhau) là:
Một người gửi tiết kiệm với lãi suất 6,5% năm và lãi hàng năm được nhập vào vốn. Hỏi khoảng bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?
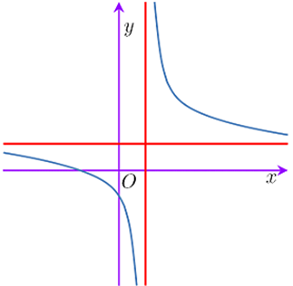
Cho hàm số \[y = \frac{{x + b}}{{cx - 1}}\] có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?