Tính tích tất cả các nghiệm của phương trình \[\log _3^2x - 2{\log _3}x - 7 = 0\].
 Giải bởi Vietjack
Giải bởi Vietjack
Điều kiện: x > 0
Đặt t = log3x phương trình trở thành t2 − 2t – 7 = 0
Có ac = 1.(−7) = −7 < 0 nên phương trình luôn có hai nghiệm t1, t2 phân biệt thỏa mãn
\[\left\{ \begin{array}{l}{t_1} + {t_2} = 2\\{t_1}{t_2} = - 7\end{array} \right.\]
Do đó phương trình đã cho luôn có hai nghiệm phân biệt \[{x_1} = {3^{{t_1}}};\,\,{x_2} = {3^{{t_2}}}\].
Khi đó \[{x_1}.{x_2} = {3^{{t_1}}}{.3^{{t_2}}} = {3^{{t_1} + {t_2}}} = {3^2} = 9\]
Vậy tích các nghiệm của phương trình đã cho bằng 9.
Tìm tất cả các giá trị của tham số m để hàm số \[y = {\log _{2020}}(mx - m + 2)\]xác định trên \[[1; + \infty )\].
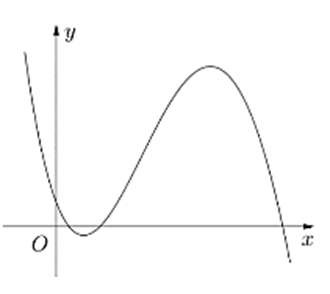
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?
Một máy bay đang bay ở độ cao 12 km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất. Nếu cách sân bay 320 km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng: AD.AB = AE.AC = HC.HB.
Cho A là tập hợp các học sinh lớp 10 đang học ở trường em và B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B; A ∩ B; A \ B; B \ A.
Cho hình bình hành ABCD, AB > AD. Hai đường chéo AC và BD cắt nhau tại O. Một đường thẳng tùy ý qua O cắt AB, CD lần lượt tai M, N. Chứng minh:
OM = ON.
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).
Tìm giá trị nhỏ nhất của biểu thức F(x; y) = y – x trên miền xác định bởi hệ bất phương trình \[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\].
Cho hàm số y=f(x) xác định trên ℝ\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
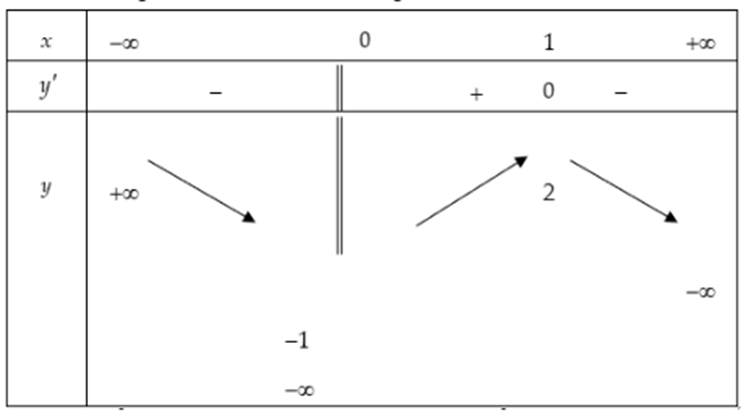
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba nghiệm thực phân biệt.
Lớp 10B có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Lý và Toán, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả Toán, Lý, Hóa. Tính số học sinh của lớp 10B.
Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích là V. Tính thể tích khối chóp A.BCC’B’.
Chứng minh hai góc kề nhau của một hình bình hành không thể có số đo là 40° và 50°.