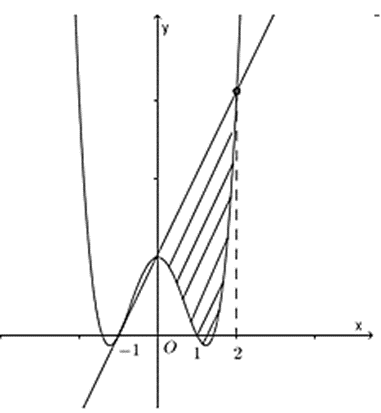
Cho hàm số y = ax4 + bx2 + c (a = 1) có đồ thị (C), biết rằng (C) đi qua A(−1; 0), tiếp tuyến d tại A của (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng \(\frac{{28}}{5}\) (phần gạch chéo trong hình vẽ). Tính diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = −1; x = 0.
Giải bởi Vietjack
Đồ thị hàm số đi qua điểm (−1; 0); (1; 0) nên ta có:
y = (x2 − 1)(x2 − m) = x4 − (1 + m)x2 + m (m > 1)
y¢ = 4x3 − 2(1 + m)x = 2x(2x2 − 1 − m)
y¢(−1) = −2(1 − m) = 2m − 2
Phương trình tiếp tuyến tại A(−1; 0) có phương trình y = (2m − 2)(x + 1)
\(\int\limits_0^2 {\left[ {\left( {2m - 2} \right)\left( {x + 1} \right) - \left( {{x^4} - \left( {1 + m} \right){x^2} + m} \right)} \right]dx} = \frac{{28}}{5}\)
\[ \Leftrightarrow \left. {\left( {2m - 2} \right)\left( {\frac{{{x^2}}}{2} + x} \right)\;} \right|_0^2 - \;\left. {\left( {\frac{{{x^5}}}{5} - \left( {1 + m} \right)\frac{{{x^3}}}{3} + mx} \right)\;} \right|_0^2 = \frac{{28}}{5}\]
\[ \Leftrightarrow 4\left( {2m - 2} \right) + \frac{8}{5} - 2m = \frac{{28}}{5}\]
Û 6m = 12 Û m = 2
Khi đó hàm số (C) có dạng: y = (x2 − 2)(x2 − 1) = x4 − 3x2 + 2
Phương trình tiếp tuyến tại A có dạng: y = 2x + 2
\(S = \int\limits_{ - 1}^0 {\left( {{x^4} - 3{x^2} + 2 - 2x - 2} \right)dx} = \int\limits_{ - 1}^0 {\left( {{x^4} - 3{x^2} - 2x} \right)dx} \)
\( = \left. {\left( {\frac{{{x^5}}}{5} - {x^3} - {x^2}} \right)\;} \right|_{ - 1}^0 = \frac{1}{5} - 1 + 1 = \frac{1}{5}\).
Cho các mệnh đề sau:
a. Nếu a // (P) thì a song song với mọi đường thẳng nằm trong (P).
b. Nếu a // (P) thì a song song với một đường thẳng nào đó nằm trong (P).
c. Nếu a // (P) thì có vô số đường thẳng nằm trong (P) và song song với a
d. Nếu a // (P) thì có một đường thẳng d nào đó nằm trong (P) sao cho a và d đồng phẳng.
Số mệnh đề đúng là:
Xác định parabol y = ax2 – bx + 1 trong mỗi trường hợp sau:
a) Có đỉnh I(−2; 37).
b) Có trục đối xứng là x = −1 và tung độ của đỉnh bằng 5.
Có bao nhiêu cách xếp 6 cặp vợ chồng ngồi xung quanh một chiếc bàn tròn, sao cho mỗi bà đều ngồi cạnh chồng của mình?
Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B. Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A. Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng.
Tính giá trị lớn nhất của hàm số \(f\left( x \right) = {e^{{x^3} - 3x + 3}}\) trên đoạn [0; 2].
Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
Có bao nhiêu cách xếp 6 nam và 6 nữ ngồi xung quanh một chiếc bàn tròn, sao cho nam và nữ ngồi xen kẽ nhau?
Tìm m để phương trình log2 x + log x − m = 0 có 2 nghiệm phân biệt thuộc khoảng (0; 1)
Cho bất phương trình 2x + 3y − 6 ≤ 0 (1). Chọn khẳng định đúng trong các khẳng định sau:
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?
Một tam giác có chiều cao bằng \(\frac{3}{4}\) cạnh đáy. Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích của nó tăng thêm 12 dm2. Tính diện tích của tam giác ban đầu.
Hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng là 80%. Xác suất người thứ hai bắn trúng là 70%. Tính xác suất để cả hai người cùng bắn trúng.
Gieo một con súc sắc cân đối và đồng chất 6 lần độc lập. Tính xác xuất để không lần nào xuất hiện mặt có số chấm là một số chẵn?
