Trong không gian với hệ tọa độ Oxyz, cho các điểm A(–1; –2; 0), B(0; –4; 0), C(0; 0; –3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A. (P): 6x – 3y + 5z = 0
B. (P): –6x + 3y + 4z = 0
C. (P): 2x – y – 3z = 0
D. (P): 2x – y + 3z = 0.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta có : \(\overrightarrow {OA} = ( - 1; - 2;0)\)
Vì (P) cách đều B, C nên \(d(B;(P)) = d(C;(P))\)
TH1: BC // (P)
\(\overrightarrow {BC} = (0;4; - 3) \Rightarrow [\overrightarrow {OA} ;\overrightarrow {BC} ] = (6; - 3; - 4){\rm{ }}\)
Suy ra (P) đi qua O và nhận \(\vec b = (6; - 3; - 4)\) là 1 VTPT
Do đó \((P):6x - 3y - 4z = 0 \Leftrightarrow (P): - 6x + 3y + 4z = 0\)
TH2: I ∈ (P), với I là trung điểm của BC
\(I\left( {0; - 2; - \frac{3}{2}} \right) \Rightarrow \overrightarrow {OI} = \left( {0; - 2; - \frac{3}{2}} \right)\)
\(\begin{array}{l} \Rightarrow [\overrightarrow {OA} ;\overrightarrow {OI} ] = \frac{1}{2}(6; - 3;4)\\ \Rightarrow (P):6x - 3y + 4z = 0\end{array}\)
Do đó có hai mặt phẳng thỏa mãn là: \( - 6x + 3y + 4z = 0\) và \(6x - 3y + 4z = 0\)
Vậy đáp án cần chọn là B.
Trong mặt phẳng α cho tứ giác ABCD, điểm E ∉ (α). Hỏi có bao nhiêu mặt phẳng phân biệt tạo bởi ba trong năm điểm A, B, C, D, E?
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là:
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB = 2a. Thể tích khối tứ diện OO'AB theo a là:
Cho tứ giác lồi ABCD và điểm S không thuộc mp(ABCD). Có bao nhiêu mặt phẳng phân biệt xác định bởi 3 trong số các điểm A, B, C, D, S?
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a. Gọi I là trung điểm cạnh AD, biết hai mặt phẳng (SBI), (SCI) cùng vuông góc với đáy và thể tích khối chóp S.ABCD bằng \(\frac{{3\sqrt {15} {a^3}}}{5}\). Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
Hai xạ thủ cùng bắn vào một tấm bia. Xác suất người thứ nhất bắn trúng là 80%. Xác suất người thứ hai bắn trúng là 70 %. Xác suất hai người cùng bắn trúng là:
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên:
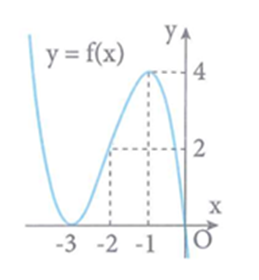
Số nghiệm thực của phương trình 2f (x2 – 1) – 5 = 0.
Có hai dãy ghế mỗi dãy xếp 5 nam, 5 nữ vào 2 dãy ghế trên. Có bao nhiêu cách nếu:
a) Nam và nữ được xếp tùy ý.
b) Nam 1 dãy ghế nữ 1 dãy ghế.
Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là đường thẳng:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, \[{\rm{A}}B = a\sqrt 3 \], AC = AA’ = a. Sin góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng:
Cho tập hợp A={1; 2; 3; 4; a; b}. Xét các mệnh đề sau đây:
(I): “3 ∈ A”.
(II): “{3; 4} ∈ A”.
(III): “{a; 3; b} ∈ A”.
Trong các mệnh đề sau, mệnh đề nào đúng?
Trong không gian cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y = f(x) = 4x2 – 4mx + m2 – 2m trên đoạn [–2; 0] bằng 3. Tính tổng T các phần tử của S.