Nghiệm của phương trình sin2x + cosx = 0 là:
A. \(\left[ \begin{array}{l}x = - \frac{\pi }{2} + k\pi \\x = - \frac{\pi }{6} + \frac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
B. \(\left[ \begin{array}{l}x = - \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{2} + \frac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
C. \(\left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{6} + \frac{{k\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
D. \(\left[ \begin{array}{l}x = - \frac{\pi }{2} + k\pi \\x = \frac{\pi }{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta có:
\(\begin{array}{l}\sin 2x + \cos x = 0\\ \Leftrightarrow 2\sin x.\cos x + \cos x = 0\\ \Leftrightarrow \cos x.(2\sin x + 1) = 0\end{array}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ c o s x = 0}\\{2 s i n x + 1 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\cos x = 0}\\{\sin x = - \frac{1}{2}}\end{array}} \right.} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k\pi }\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{2} + \frac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vậy ta chọn đáp án B.
Trong mặt phẳng α cho tứ giác ABCD, điểm E ∉ (α). Hỏi có bao nhiêu mặt phẳng phân biệt tạo bởi ba trong năm điểm A, B, C, D, E?
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là:
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB = 2a. Thể tích khối tứ diện OO'AB theo a là:
Cho tứ giác lồi ABCD và điểm S không thuộc mp(ABCD). Có bao nhiêu mặt phẳng phân biệt xác định bởi 3 trong số các điểm A, B, C, D, S?
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a. Gọi I là trung điểm cạnh AD, biết hai mặt phẳng (SBI), (SCI) cùng vuông góc với đáy và thể tích khối chóp S.ABCD bằng \(\frac{{3\sqrt {15} {a^3}}}{5}\). Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
Hai xạ thủ cùng bắn vào một tấm bia. Xác suất người thứ nhất bắn trúng là 80%. Xác suất người thứ hai bắn trúng là 70 %. Xác suất hai người cùng bắn trúng là:
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên:
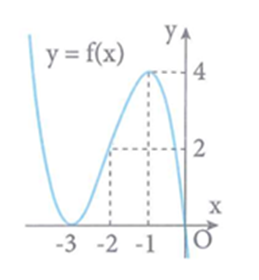
Số nghiệm thực của phương trình 2f (x2 – 1) – 5 = 0.
Có hai dãy ghế mỗi dãy xếp 5 nam, 5 nữ vào 2 dãy ghế trên. Có bao nhiêu cách nếu:
a) Nam và nữ được xếp tùy ý.
b) Nam 1 dãy ghế nữ 1 dãy ghế.
Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là đường thẳng:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, \[{\rm{A}}B = a\sqrt 3 \], AC = AA’ = a. Sin góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng:
Cho tập hợp A={1; 2; 3; 4; a; b}. Xét các mệnh đề sau đây:
(I): “3 ∈ A”.
(II): “{3; 4} ∈ A”.
(III): “{a; 3; b} ∈ A”.
Trong các mệnh đề sau, mệnh đề nào đúng?
Trong không gian cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y = f(x) = 4x2 – 4mx + m2 – 2m trên đoạn [–2; 0] bằng 3. Tính tổng T các phần tử của S.