Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu?
A. \(r = \sqrt[3]{{\frac{{V\pi }}{2}}}\)
B. \(r = \sqrt[3]{V}\)
C. \(r = \sqrt[3]{{\frac{V}{{2\pi }}}}\)
D. \(r = \sqrt[3]{{\frac{V}{2}}}\).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Ta có \({S_{{\rm{day }}}} = \pi {r^2};{S_{xq}} = 2\pi rh\)
Thể tích khối trụ là: \(V = {S_{{\rm{day }}}}.h \Rightarrow h = \frac{V}{{{S_{day}}}} = \frac{V}{{\pi {r^2}}}\)
Ta có: \({S_{tp}} = 2{S_{day}} + {S_{xq}} = 2\pi {r^2} + 2\pi rh = 2\pi {r^2} + 2\pi r \cdot \frac{V}{{\pi {r^2}}} = 2\pi {r^2} + \frac{{2V}}{r}\)
Xét hàm số \(f(r) = 2\pi {r^2} + \frac{{2V}}{r}\), có :
\(f'(r) = 4\pi r - \frac{{2V}}{{{r^2}}}\)
\(f'(r) = 0 \Leftrightarrow 4\pi r = \frac{{2V}}{{{r^2}}} \Leftrightarrow r = \sqrt[3]{{\frac{V}{{2\pi }}}}\)
Ta có bảng biến thiên
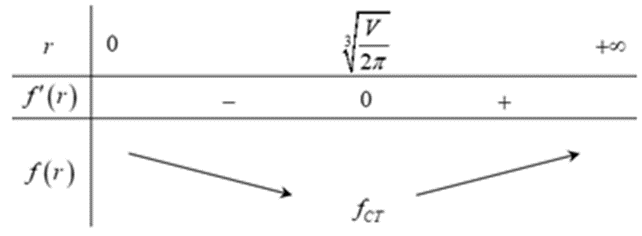
Suy ra giá trị nhỏ nhất của hàm số đạt tại \(r = \sqrt[3]{{\frac{V}{{2\pi }}}}\)
Do đó khi \(r = \sqrt[3]{{\frac{V}{{2\pi }}}}\) thì diện tích toàn phần hình trụ đạt giá trị nhỏ nhất
Vậy ta chọn đáp án C.
Trong mặt phẳng α cho tứ giác ABCD, điểm E ∉ (α). Hỏi có bao nhiêu mặt phẳng phân biệt tạo bởi ba trong năm điểm A, B, C, D, E?
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là:
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB = 2a. Thể tích khối tứ diện OO'AB theo a là:
Cho tứ giác lồi ABCD và điểm S không thuộc mp(ABCD). Có bao nhiêu mặt phẳng phân biệt xác định bởi 3 trong số các điểm A, B, C, D, S?
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a. Gọi I là trung điểm cạnh AD, biết hai mặt phẳng (SBI), (SCI) cùng vuông góc với đáy và thể tích khối chóp S.ABCD bằng \(\frac{{3\sqrt {15} {a^3}}}{5}\). Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
Hai xạ thủ cùng bắn vào một tấm bia. Xác suất người thứ nhất bắn trúng là 80%. Xác suất người thứ hai bắn trúng là 70 %. Xác suất hai người cùng bắn trúng là:
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên:
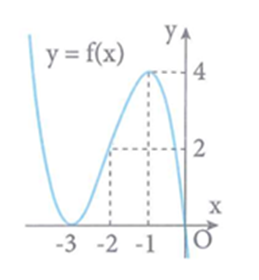
Số nghiệm thực của phương trình 2f (x2 – 1) – 5 = 0.
Có hai dãy ghế mỗi dãy xếp 5 nam, 5 nữ vào 2 dãy ghế trên. Có bao nhiêu cách nếu:
a) Nam và nữ được xếp tùy ý.
b) Nam 1 dãy ghế nữ 1 dãy ghế.
Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là đường thẳng:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, \[{\rm{A}}B = a\sqrt 3 \], AC = AA’ = a. Sin góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng:
Cho tập hợp A={1; 2; 3; 4; a; b}. Xét các mệnh đề sau đây:
(I): “3 ∈ A”.
(II): “{3; 4} ∈ A”.
(III): “{a; 3; b} ∈ A”.
Trong các mệnh đề sau, mệnh đề nào đúng?
Trong không gian cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y = f(x) = 4x2 – 4mx + m2 – 2m trên đoạn [–2; 0] bằng 3. Tính tổng T các phần tử của S.