Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AC. Qua A kẻ Ax song song với BC cắt HI tại K. Khi đó HK song song với:
Giải bởi Vietjack
Đáp án đúng là: A
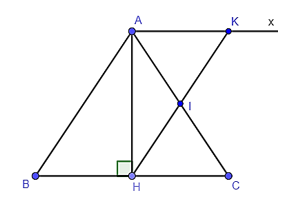
Vì tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến.
Suy ra H là trung điểm của BC.
Trong tam giác ABC có H là trung điểm của BC, I là trung điểm của AC.
Do đó HI là đường trung bình của tam giác ABC.
Suy ra HI // AB (tính chất đường trung bình của tam giác).
Vì K ∈ HI nên HK // AB.
Cho tam giác ABC trên nửa mặt phẳng bờ AC không chứa điểm B lấy điểm D bất kì. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, AD, DC. Khi đó EF + FH + HG + GE bằng
Cho tứ giác ABCD có AB = 2a, CD = 2b. Gọi E, F lần lượt là trung điểm của AD, BC. Khẳng định nào sau đây là đúng?
Cho tam giác ABC đều, I là trung điểm BC. Từ I kẻ IK // AB (K ∈ AC), IH // AC (H ∈ AB). Tam giác IHK là tam giác gì?
Cho tam giác MNP cân tại M có D là trung điểm của NP. Từ D kẻ DE song song với MP (E ∈ MN), kẻ DF song song với MN (F ∈ MP). Khi đó ME bằng với đoạn thẳng nào?
Cho tam giác ABC, các đường trung tuyến BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Đoạn thẳng DE song song và bằng với đoạn thẳng nào?
Cho tam giác ABC, AB = 4 cm, AC = 6 cm, BC = 8 cm. Kéo dài AB lấy điểm D sao cho AB = BD, kéo dài AC lấy điểm E sao cho AC = CE, kéo dài trung tuyến AM của tam giác ABC lấy F sao cho AM = MF. Khẳng định nào sau đây là đúng?
Cho tam giác OMN cân tại O. I là trung điểm của đường cao OH, NI cắt OM tại K. Từ H kẻ Hx song song với NK cắt OM tại D. Khi đó độ dài OM gấp mấy lần độ dài OK?
Cho tam giác MNP, trên MN lấy hai điểm D, E sao cho MD = DE = EN. Gọi I là trung điểm NP, PD cắt MI tại H. Khẳng định nào sau đây là đúng?
Cho tam giác ABC vuông tại B, phân giác AD. Gọi M, N, I lần lượt là trung điểm của AD, AC, CD. Tứ giác BMNI là hình gì?
