Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam giác đồng dạng?
A. 4;
B. 6;
C. 8;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D
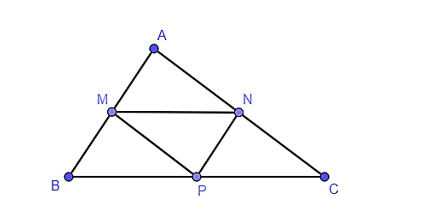
Vì M, N lần lượt là trung điểm của AB, AC.
Suy ra MN là đường trung bình của tam giác ABC nên MN // BC.
Vì M, P lần lượt là trung điểm của AB, BC.
Suy ra MP là đường trung bình của tam giác ABC nên MP // AC.
Vì N, P lần lượt là trung điểm của AC, BC.
Suy ra NP là đường trung bình của tam giác ABC nên NP // AB.
Xét tam giác ABC:
+ Do MN // BC nên ΔAMN ᔕ ΔABC.
+ Do MP // AC nên ΔMBP ᔕ ΔABC.
+ Do NP // AB nên ΔNPC ᔕ ΔABC.
Vì ΔAMN ᔕ ΔABC, ΔMBP ᔕ ΔABC, ΔNPC ᔕ ΔABC nên các tam giác AMN, MBP, NPC đôi một đồng dạng với nhau.
Xét hai tam giác AMN và PNM có:
AM = PN
MN: Cạnh chung
MP = AN
Suy ra ΔAMN = ΔPNM (c – c – c).
Do đó, ΔAMN ᔕ ΔPNM.
Từ đó suy ra 5 tam giác AMN, PNM, MBP, NPC, ABC đôi một đồng dạng với nhau.
Vậy có tất cả 10 cặp tam giác đồng dạng.
Cho tam giác ABC và các điểm M, N lần lượt trên các cạnh AB, AC sao cho MN // BC. Khẳng định nào sau đây là đúng?
Cho hình sau, hãy chỉ ra hai tam giác đồng dạng và tỉ số đồng dạng của hai tam giác đó.
Cho hình bình hành ABCD. Lấy E trên cạnh BC, tia DE cắt AB tại F. Khi đó tam giác FBE đồng dạng với tam giác nào dưới đây?
Cho tứ giác MNPQ. Đường chéo NQ chia tứ giác thành hai tam giác đồng dạng với nhau là ΔMNQ và ΔNQP. Khẳng định nào sau đây là đúng?
Cho tam giác ABC, DE // BC (D ∈ AB, E ∈ AC). Biết AB = 5 cm, BC = 9 cm, AD = 2 cm, độ dài của ED là: