Cho hình bình hành ABCD có AC > BD. Kẻ CE ⊥ AB tại E, CF ⊥ AD tại F, BH ⊥ AC tại H và DK ⊥ AC tại K. Khẳng định nào sau đây là đúng?
A. AD ⋅ AB + AE ⋅ AF = AC2;
B. AB ⋅ AF + AE ⋅ AD = AC2;
C. AD ⋅ AF + AE ⋅ AB = AC2;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C
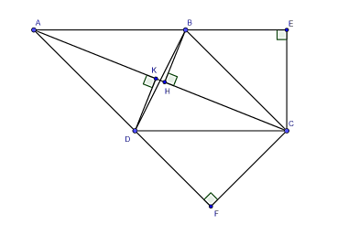
Xét tam giác AKD vuông tại K và tam giác CHB vuông tại H có:
AD = BC (do ABCD là hình bình hành)
(AD // BC, hai góc so le trong)
Do đó, ∆AKD = ∆CHB (cạnh huyền – góc nhọn).
Suy ra AK = HC.
Xét hai tam giác AHB và AEC có:
: Góc chung
Do đó, ΔAHB ᔕ ΔAEC (g – g).
Suy ra .
Suy ra AB ⋅ AE = AC ⋅ AH (1).
Xét hai tam giác ADK và ACF có
: Góc chung
Do đó, ΔADK ᔕ ΔACF (g – g).
Suy ra .
Suy ra AD ⋅ AF = AC ⋅ AK (2).
Lấy (1) + (2) ta được AB ⋅ AE + AD ⋅ AF = AC ⋅ AH + AC ⋅ AK
Lại có AC ⋅ AH + AC ⋅ AK = AC ⋅ (AH + AK) = AC ⋅ (AH + HC) = AC ⋅ AC = AC2.
Vậy AB ⋅ AE + AD ⋅ AF = AC2.
Cho tam giác ABC có AM là phân giác trong của tam giác. Kẻ tia Cx thuộc nửa mặt phẳng bờ BC không chứa A sao cho . Gọi N là giao điểm của Cx và AM. Khẳng định nào sau đây là đúng?
Cho tam giác ABC có đường phân giác trong AD. Gọi M và N theo thứ tự là hình chiếu của B và C trên đường thẳng AD. Khi đó tỉ số bằng tỉ số
Cho hình bình hành ABCD. Một đường thẳng bất kì đi qua A cắt BD tại E và cắt các đường thẳng BC, CD lần lượt tại F và G. Trong các khẳng định sau, khẳng định nào là sai?
Cho tam giác ABC và d là đường thẳng tùy ý qua B. Qua E là điểm bất kì trên AC, vẽ đường thẳng song song với AB và BC, lần lượt cắt d tại M và N. Gọi D là giao điểm của ME và BC. Đường thẳng NE cắt AB và MC lần lượt tại F và K. Khi đó tam giác AFN đồng dạng với tam giác nào dưới đây?
Cho hình thang ABCD (AB // CD) có . Biết AB = 12 cm, DC = 18 cm. Độ dài BD (làm tròn đến hàng phần mười) là