Cho ΔABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF. Gọi G là trọng tâm tam giác ABC. Tia AG cắt BC tại M. Khẳng định nào sau đây là đúng?
A. Hai tam giác ABC và AEF có cùng trọng tâm;
B. Hai tam giác ABC và AEC có cùng trọng tâm;
C. Hai tam giác ABC và ABF có cùng trọng tâm;
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A
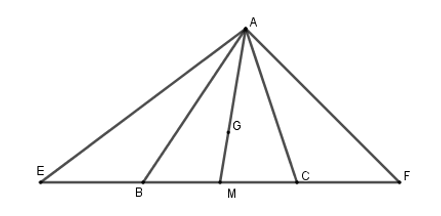
Ta có: G là trọng tâm của tam giác ABC nên AG là trung tuyến của tam giác
Mà AG cắt BC tại M nên M là trung điểm của BC
Do đó MB = MC.
Lại có BE = CF (giả thiết)
Nên MB + BE = MC + CF hay ME = MF.
Suy ra AM là đường trung tuyến ứng với cạnh EF của ΔAEF.
Mặt khác (do G là trọng tâm của ΔABC).
Do đó G là trọng tâm của ΔAEF
Mà G là trọng tâm của ΔABC, nên hai tam giác ABC và AEF có cùng trọng tâm là điểm G.
Vậy ta chọn phương án A.
Cho ΔABC có đường trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho và G là trung điểm của BK. Gọi E là trung điểm CK; GE cắt AC tại I. Số thích hợp để điền vào chỗ trống CI = … AC là:
Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Gọi M, N lần lượt là trung điểm của BC, CD. Đoạn thẳng AM, AN cắt BD lần lượt tại I và K. Khẳng định nào sau đây là đúng?
Cho tam giác ΔABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm E và F sao cho AE = EF = FD. Điểm F là:
Cho ∆ABC, điểm M thuộc cạnh BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khi đó điểm M là
Cho ∆ABC có AD, BE, CF là ba đường trung tuyến cắt nhau tại G. Cho các phát biểu sau:
(I)
(II) AD + BE + CF < AB + BC + AC.
Chọn khẳng định đúng:
Cho tam giác ABC, trên đường trung tuyến AD. Gọi G là điểm nằm giữa A và D sao cho Tia BG cắt AC tại E, tia CG cắt AB tại F. Khẳng định nào sau đây sai?
Cho ΔABC có đường trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho và G là trung điểm của BK. Gọi E là trung điểm của CK, GE cắt AC tại I. Điểm I là trọng tâm của tam giác nào?
Cho hình vẽ như bên dưới. Biết AM = 12 cm.
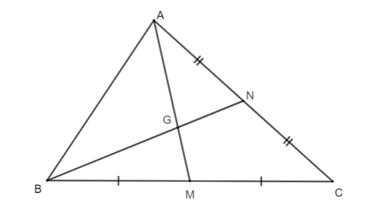
Độ dài của đoạn thẳng AG là
