Cho ΔABC có I là giao điểm của hai tia phân giác của góc A và B. Qua I kẻ đường thẳng song song với BC, cắt AB tại M, cắt AC tại N. Khẳng định nào sau đây là đúng?
A. MN = BM + CN;
B. MN > BM + CN;
C. MN < BM + CN;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A
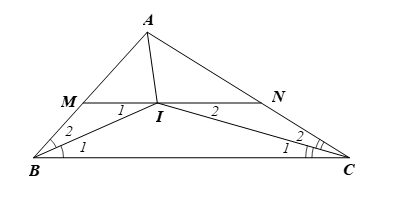
Xét ∆ABC có I là giao điểm của hai tia phân giác và nên CI là tia phân giác của
Vì MN // BC nên (hai góc so le trong)
Mà nên
Do đó ΔNIC cân tại N nên NC = NI. (1)
Tương tự, ta có: MB = MI. (2)
Từ (1) và (2) ta có: MI + IN = BM + CN hay MN = BM + CN.
Cho ΔABC, các tia phân giác của góc B và C cắt nhau ở I. Biết số đo của góc BAC là
Cho ΔABC có các tia phân giác của và cắt nhau tại I. Gọi D, E là chân đường vuông góc hạ từ I đến các cạnh AB và AC. Biết ID = x – 3 và IE = 2x + 3. Giá trị của x là
Cho ΔABC có và hai đường phân giác AD, BE (D ∈ BD, E ∈ AC). Số đo của là
Cho ΔMNP vuông tại M, các tia phân giác của góc N và góc P cắt nhau tại I. Gọi D, E là chân các đường vuông góc hạ từ I đến các cạnh MN và MP. Biết ID = 5 cm, độ dài cạnh IE là
Cho tam giác ABC có M là trung điểm của cạnh BC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm E của AB cắt BC tại U, đường thẳng qua D và trung điểm F của AC cắt BC tại V. Khẳng định nào sau đây là sai?
Cho hình vẽ. Biết CI và BI lần lượt là đường phân giác của và
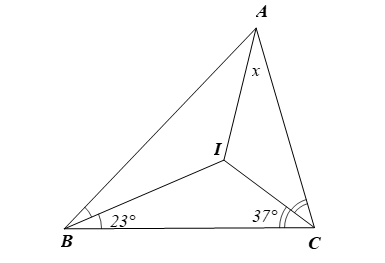
Giá trị của x là
Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Cho các khẳng định sau:
(I) IM = IN = IP;
(II)
(III) IA = IB = IC.
Có bao nhiêu khẳng định đúng?
Cho tam giác ABC có 2 đường trung tuyến AE và BF cắt nhau tại I. Cho 2 điểm M và N lần lượt là trung điểm của IA và IB. Khẳng định nào sau đây đúng?
Tam giác ABC có trung tuyến AM = 9 cm và trọng tâm G. Độ dài đoạn AG là