10 câu hỏi trắc nghiệm thuộc Dạng 6. Chứng minh đoạn thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc

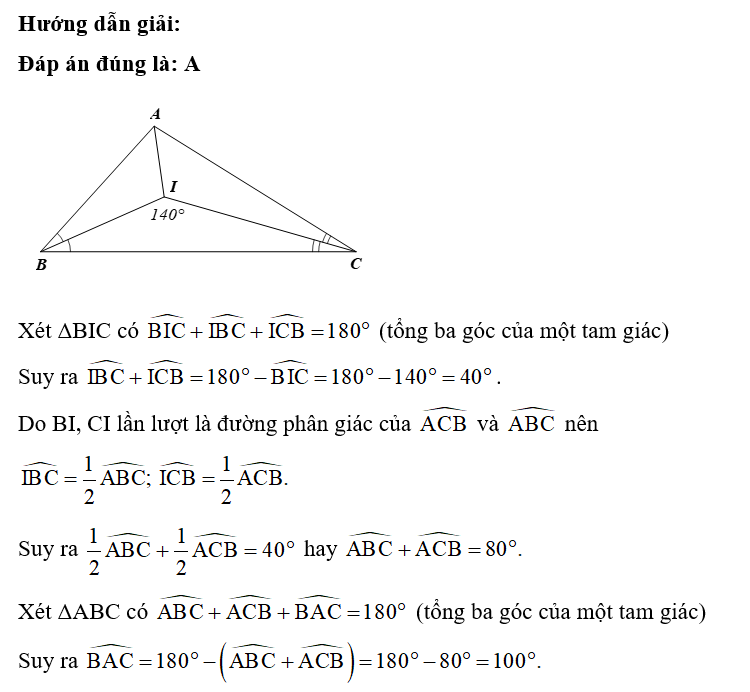
Trắc nghiệm Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án

Dạng 6. Chứng minh đoạn thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc

147 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tam giác ABC có trung tuyến AM = 9 cm và trọng tâm G. Độ dài đoạn AG là

A. 4,5 cm;

B. 3 cm;

C. 6 cm;

D. 8 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

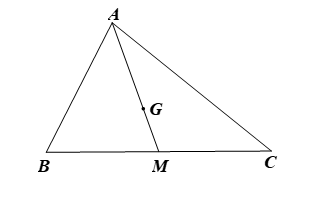
Tam giác ABC có trung tuyến AM = 9 cm và trọng tâm G. Độ dài đoạn AG là A. 4,5 cm; B. 3 cm; C. 6 cm; D. 8 cm. (ảnh 1)

Vì G là trọng tâm ΔABC và AM là đường trung tuyến nên $A G = \frac{2}{3} A M = \frac{2}{3} .9 = 6$ (cm).

Câu 2:

Cho ΔMNP vuông tại M, các tia phân giác của góc N và góc P cắt nhau tại I. Gọi D, E là chân các đường vuông góc hạ từ I đến các cạnh MN và MP. Biết ID = 5 cm, độ dài cạnh IE là

A. 5 cm;

B. 3 cm;

C. 6 cm;

D. 8 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

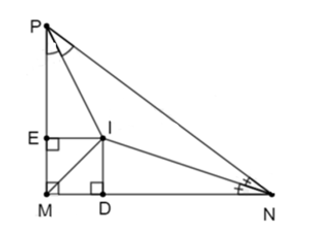
Cho tam giác MNP vuông tại M, các tia phân giác của góc N và góc P cắt nhau tại I. Gọi D, E là chân (ảnh 1)

Xét tam giác MNP có các tia phân giác góc N và góc P cắt nhau tại I nên I là giao điểm của ba đường phân giác trong ΔMNP.

Khi đó IE = ID = 5 cm (tính chất ba đường phân giác của tam giác).

Câu 3:

Cho tam giác ABC có 2 đường trung tuyến AE và BF cắt nhau tại I. Cho 2 điểm M và N lần lượt là trung điểm của IA và IB. Khẳng định nào sau đây đúng?

A. IN = IM;

B. IE = IB;

C. AI = BI;

D. IN = IF.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

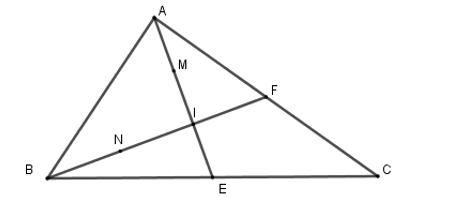
Cho tam giác ABC có 2 đường trung tuyến AE và BF cắt nhau tại I. Cho 2 điểm M và N lần lượt là (ảnh 1)

Xét ∆ABC có I là giao điểm của 2 đường trung tuyến nên I là trọng tâm của ∆ABC.

Suy ra $I B = \frac{2}{3} B F$ nên $I F = \frac{1}{2} I B$ .

Lại có N là trung điểm của IB suy ra $I N = \frac{1}{2} I B$ .

Vậy IN = IF.

Câu 4:

Cho hình vẽ. Biết CI và BI lần lượt là đường phân giác của $\hat{A C B}$ và $\hat{A B C}$

Giá trị của x là

A. 120°;

B. 60°;

C. 30°;

D. 45°.

Xem đáp án

Cho hình vẽ. Biết CI và BI lần lượt là đường phân giác của góc ACB và góc ABC Giá trị của x là (ảnh 2)

Câu 5:

Cho ΔABC, các tia phân giác của góc B và C cắt nhau ở I. Biết $\hat{B I C} = 140 °,$ số đo của góc BAC là

A. 100°;

B. 60°;

C. 30°;

D. 45°.

Xem đáp án

Cho ΔABC, các tia phân giác của góc B và C cắt nhau ở I. Biết góc BIC = 140 độ số đo của góc BAC là (ảnh 1)

Câu 6:

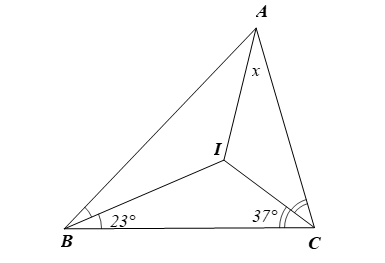
Cho ΔABC có $\hat{A} = 90 °,$ các tia phân giác của $\hat{B}$ và $\hat{C}$ cắt nhau tại I. Gọi D, E là chân đường vuông góc hạ từ I đến các cạnh AB và AC. Biết ID = x – 3 và IE = 2x + 3. Giá trị của x là

A. 5 cm;

B. 7 cm;

C. 6 cm;

D. 8 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

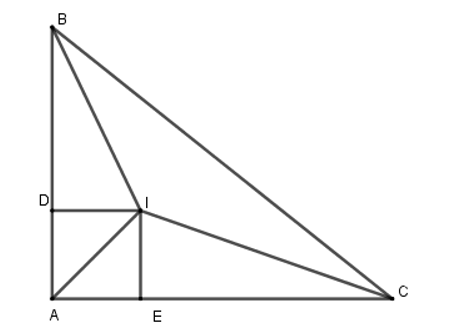
Cho tam giác ABC có góc A = 90 độ các tia phân giác của góc B và góc C cắt nhau tại I. Gọi D, E là chân (ảnh 1)

Xét ∆ABC có I là giao điểm các đường phân giác trong của góc B và C nên AI là tia phân giác của góc BAC.

Suy ra ID = IE (tính chất tia phân giác).

Do đó: x – 3 = 2x – 9

Hay 2x – x = 9 – 3.

Vậy: x = 6 (cm).

Câu 7:

Cho ΔABC có I là giao điểm của hai tia phân giác của góc A và B. Qua I kẻ đường thẳng song song với BC, cắt AB tại M, cắt AC tại N. Khẳng định nào sau đây là đúng?

A. MN = BM + CN;

B. MN > BM + CN;

C. MN < BM + CN;

M N = \frac{1}{2} (B M + C N)

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

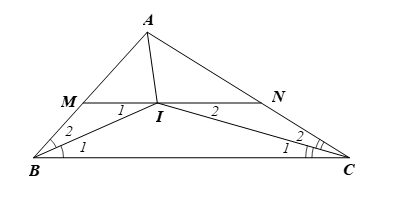
Cho ΔABC có I là giao điểm của hai tia phân giác của góc A và B. Qua I kẻ đường thẳng (ảnh 1)

Xét ∆ABC có I là giao điểm của hai tia phân giác $\hat{A}$ và $\hat{B}$ nên CI là tia phân giác của $\hat{C}$

Vì MN // BC nên ${\hat{C}}_{1} = {\hat{I}}_{2}$ (hai góc so le trong)

Mà ${\hat{C}}_{1} = \hat{C_{2}}$ nên ${\hat{C}}_{2} = {\hat{I}}_{2}$

Do đó ΔNIC cân tại N nên NC = NI. (1)

Tương tự, ta có: MB = MI. (2)

Từ (1) và (2) ta có: MI + IN = BM + CN hay MN = BM + CN.

Câu 8:

Cho ΔABC có $\hat{A} = 120 °$ và hai đường phân giác AD, BE (D ∈ BD, E ∈ AC). Số đo của $\hat{B E D}$ là

A. 120°;

B. 60°;

C. 30°;

D. 45°.

Xem đáp án

Cho ΔABC có góc A= 120 độ và hai đường phân giác AD, BE (D thuộc BD, E thuộc AC). Số đo của góc BED là (ảnh 1)

Câu 9:

Cho tam giác ABC có M là trung điểm của cạnh BC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm E của AB cắt BC tại U, đường thẳng qua D và trung điểm F của AC cắt BC tại V. Khẳng định nào sau đây là sai?

A. BU = UV;

B. BU = VC;

C. $U M = \frac{2}{3} B M;$

U V = \frac{2}{3} B M .

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

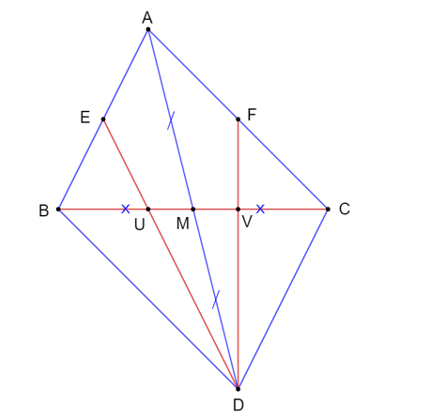
Cho tam giác ABC có M là trung điểm của cạnh BC và D là điểm sao cho M là trung điểm của (ảnh 1)

⦁ Tam giác BAC có M là trung điểm của BC nên suy ra MB = MC (1)

Xét ∆ABD có U là giao của hai đường trung tuyến BM và DE nên U là trọng tâm của ∆ABD.

Suy ra $B U = \frac{2}{3} B M$ (2)

Từ đó ta có: $U M = B M - B U = B M - \frac{2}{3} B M = \frac{1}{3} B M$ (3)

Do đó khẳng định C là sai. Đến đây ta có thể chọn phương án C.

⦁ Xét phương án D:

Xét ∆ACD có V là giao của hai đường trung tuyến CM và DF nên V là trọng tâm của ∆ACD.

Suy ra $C V = \frac{2}{3} C M$ (4)

Từ đó ta có: $M V = C M - C V = C M - \frac{2}{3} C M = \frac{1}{3} C M$ (5)

Từ (1), (3), (5) ta có: $U V = U M + M V = \frac{1}{3} M B + \frac{1}{3} M C = \frac{2}{3} M B$ (6)

Do đó khẳng định D là đúng.

⦁ Xét phương án A và B:

Từ (1), (2), (4), (6) ta có: $B U = U V = V C = \frac{2}{3} M B$ .

Do đó khẳng định A và B là đúng.

Vậy ta chọn phương án C.

Câu 10:

Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Cho các khẳng định sau:

(I) IM = IN = IP;

(II) $\hat{N I H} = \hat{P I A};$

(III) IA = IB = IC.

Có bao nhiêu khẳng định đúng?

A. 0;

B. 1;

C. 2;

D. 3.

Xem đáp án

Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Cho các khẳng định sau: (ảnh 1)

Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Cho các khẳng định sau: (ảnh 2)

Bắt đầu thi ngay