10 câu hỏi trắc nghiệm thuộc Dạng 5. Chứng minh ba đường đồng quy, ba điểm thẳng hàng

Câu 1:

Khẳng định nào sau đây là đúng?

A. Ba đường trung tuyến của một tam giác cùng đi qua một điểm;

B. Ba đường trung tuyến của một tam giác không cắt nhau;

C. Ba đường trung tuyến của một tam giác luôn vuông góc với nhau;

D. Ba đường trung tuyến của một tam giác song song với nhau.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm).

Câu 2:

Khẳng định nào sau đây là đúng?

A. Ba đường phân giác của một tam giác không đồng quy tại một điểm;

B. Ba đường phân giác của một tam giác đồng quy tại một điểm, điểm này cách đều ba đỉnh của tam giác đó;

C. Ba đường phân giác của một tam giác đồng quy tại một điểm, điểm này cách đều ba cạnh của tam giác đó;

D. Cả A, B, C đều sai.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Ba đường phân giác của một tam giác đồng quy tại một điểm, điểm này cách đều ba cạnh của tam giác đó.

Câu 3:

Cho tam giác MNP cân tại M có G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Khẳng định nào sau đây là sai?

A. I là giao điểm ba đường phân giác của ΔMNP;

B. MI là đường trung tuyến của ΔMNP;

C. Ba điểm M, G, I thẳng hàng;

D. MG = NG.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là:D

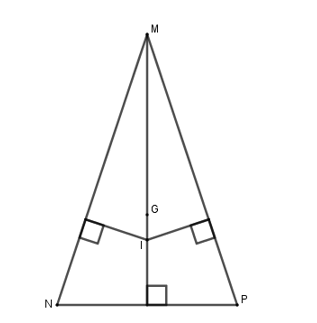
Cho tam giác MNP cân tại M có G là trọng tâm, I là điểm nằm trong tam giác và cách đều (ảnh 1)

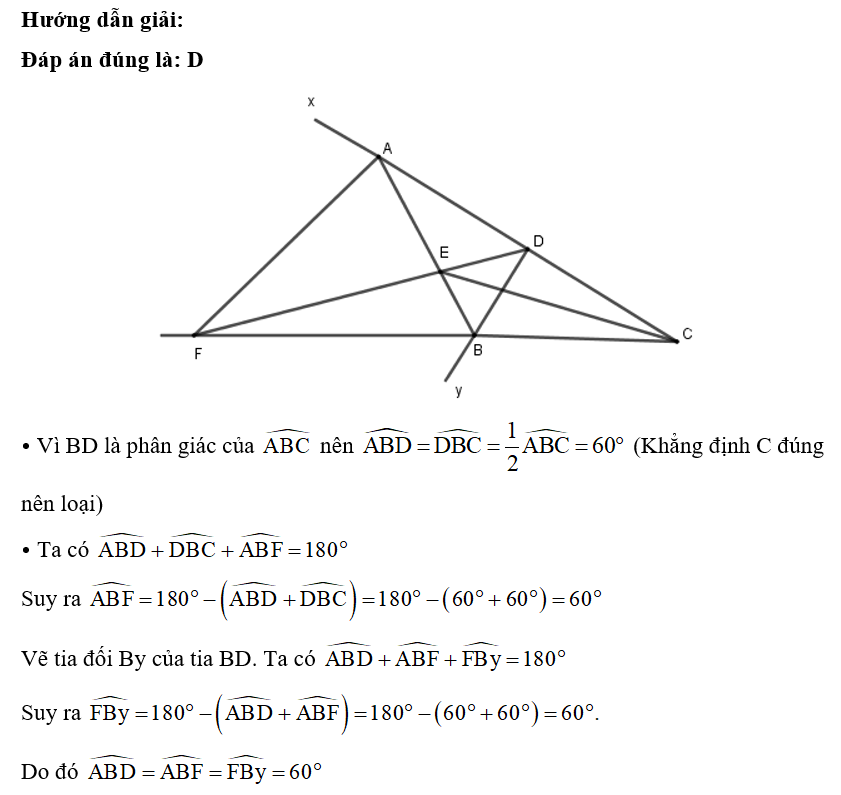
Điểm I nằm trong ΔMNP và cách đều ba cạnh của tam giác nên I là giao điểm của ba đường phân giác, suy ra MI là tia phân giác của Do đó khẳng định A là đúng.

Do ΔMNP cân tại M nên đường phân giác MI cũng là trung tuyến. Do đó khẳng định B là đúng.

G là trọng tâm của ΔMNP nên G nằm trên đường trung tuyến MI.

Từ đó suy ra ba điểm M, G, I thẳng hàng. Do đó khẳng định C là đúng.

Vậy ta chọn phương án D.

Câu 4:

Cho tam giác ABC, ba đường trung tuyến AD, BE và CF cắt nhau tại G. Trên BE, CF lần lượt lấy các điểm M và N sao cho $B M = \frac{1}{3} B E, C N = \frac{1}{3} C F$ . Khẳng định nào sau đây là sai?

A. $G B = \frac{2}{3} B E$ ;

B. GD, BN và CM đồng quy;

C. CN = NG;

D.

G E = \frac{2}{3} B E

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

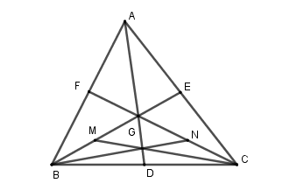
Cho tam giác ABC, ba đường trung tuyến AD, BE và CF cắt nhau tại G. Trên BE, CF lần lượt lấy (ảnh 1)

ΔABC có ba đường trung tuyến AD, BE và CF cắt nhau tại G nên G là trọng tâm của ΔABC nên $G B = \frac{2}{3} B E$ và $G E = \frac{1}{3} B E .$ Do đó khẳng định A là đúng, D là sai.

Mặt khác $B M = \frac{1}{3} B E$ nên BM = MG.

Chứng minh tương tự, ta được CN = NG. Do đó khẳng định C là đúng.

Xét ΔGBC có GD, BN và CM là ba đường trung tuyến nên đồng quy tại một điểm. Do đó khẳng định B là đúng.

Vậy ta chọn phương án D.

Câu 5:

Cho tam giác ABC cân tại A có đường trung tuyến AD và đường phân giác CF. Trên cạnh AC lấy điểm E sao cho AE = AF. Khẳng định nào sau đây là đúng?

A. ΔABE cân;

B. ΔACF cân;

C. Ba đường AD, BE, CF đồng quy;

D. BE là đường trung tuyến của ΔABC.

Xem đáp án

Cho tam giác ABC cân tại A có đường trung tuyến AD và đường phân giác CF. Trên cạnh AC (ảnh 1)

Câu 6:

Cho ΔABC có điểm I cách đều ba cạnh của tam giác. Gọi N là giao điểm của hai tia phân giác góc ngoài tại B và C. Khi đó ta có:

A. Ba điểm A, I, N thẳng hàng;

B. Điểm I là giao điểm của ba đường trung tuyến của ΔABC;

C. AN là đường phân giác của góc ngoài tại đỉnh A của ΔABC;

D. Cả A, B, C đều đúng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

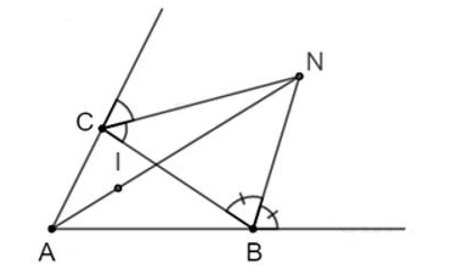
Cho tam giác ABC có điểm I cách đều ba cạnh của tam giác. Gọi N là giao điểm của hai tia phân giác (ảnh 1)

Ta có: hai tia phân giác góc ngoài tại B và C của ΔABC cắt nhau tại N nên AN là tia phân giác của $\hat{B A C}$ (Theo kết quả của Ví dụ 3) (1)

ΔABC có: điểm I cách đều ba cạnh của tam giác nên I là giao điểm của ba đường phân giác của ΔABC.

Khi đó AI là tia phân giác của $\hat{B A C}$ (2)

Từ (1) và (2) suy ra A, I, N thẳng hàng.

Câu 7:

Cho tam giác ABC, tia phân giác AD. Các đường phân giác ngoài tại đỉnh B và C cắt nhau ở E. Khẳng định nào sau đây là sai?

A. AD, BE, CE đồng quy;

B. Ba điểm A, D, E thẳng hàng;

C. ΔEBC cân;

D. E cách đều ba đường thẳng chứa ba cạnh của tam giác.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

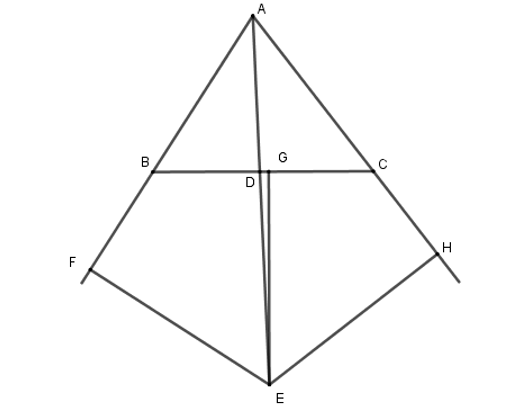
Cho tam giác ABC, tia phân giác AD. Các đường phân giác ngoài tại đỉnh B và C cắt nhau ở E. Khẳng định nào sau đây là sai? (ảnh 1)

Ta có E là giao điểm của hai đường phân giác ngoài tại đỉnh B và C nên theo kết quả của Ví dụ 3, ta có AE là tia phân giác của góc BAC.

Mà AD là tia phân giác của góc BAC

Do đó ba điểm A, D, E thẳng hàng hay AD, BE, CE đồng quy và E cách đều ba đường thẳng chứa ba cạnh của tam giác.

Vậy các khẳng định A, B, D đều đúng. Ta chọn phương án C.

Câu 8:

Cho tam giác ABC có $\hat{B} = 120 ° .$ Vẽ các đường phân giác BD, CE. Đường thẳng chứa tia phân giác ngoài tại đỉnh A của tam giác ABC cắt đường thẳng BC tại F. Khẳng định nào sau đây là sai?

A. $\hat{A D F} = \hat{B D F};$

B. Ba điểm D, E, F thẳng hàng;

C. $\hat{A B D} = 60 °;$

D.

\hat{F B D} > \hat{A B C} .

Xem đáp án

Cho tam giác ABC có góc B = 120 độ. Vẽ các đường phân giác BD, CE. Đường thẳng chứa tia phân (ảnh 1)

Cho tam giác ABC có góc B = 120 độ. Vẽ các đường phân giác BD, CE. Đường thẳng chứa tia phân (ảnh 2)

Câu 9:

Cho tam giác ABC. Các đường phân giác của các góc ngoài của tam giác cắt nhau tại D, E, F (D nằm trong góc A, E nằm trong góc B, F nằm trong góc C). Khẳng định nào sau đây là đúng?

A. AD là đường trung tuyến của ΔABC;

B. BF và CE không cắt nhau;

C. AD và BE không cắt nhau;

D. Ba đường AD, BE, CF đồng quy.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

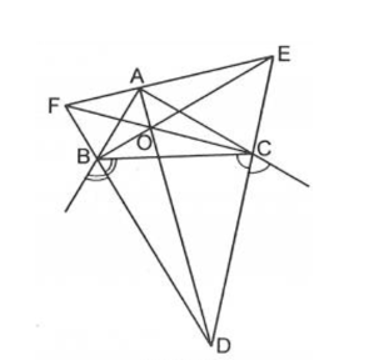
Cho tam giác ABC. Các đường phân giác của các góc ngoài của tam giác cắt nhau tại D, E, F (ảnh 1)

Xét ΔABC, các đường phân giác ngoài tại đỉnh B và đỉnh C cắt nhau tại D.

Suy ra AD là đường phân giác trong tại đỉnh A (theo kết quả của Ví dụ 3).

Chứng minh tương tự ta được BE, CF lần lượt là các đường phân giác trong tại đỉnh B, đỉnh C của ΔABC.

Do đó, ba đường AD, BE, CF đồng quy tại một điểm.

Câu 10:

Cho tam giác MNP cân tại P. Hai đường trung tuyến MH và NK cắt nhau tại G. Kéo dài PG cắt MN tại I. Gọi E, F lần lượt là trung điểm của GP và GM. Trong các khẳng định sau có bao nhiêu khẳng định đúng?

(I) Các đường thẳng PF, GK, ME đồng quy;

(II) DPIN = DPIM;

(III) G là trọng tâm tam giác MNP;

A. 0;

B. 1;

C. 2;

D. 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là:D

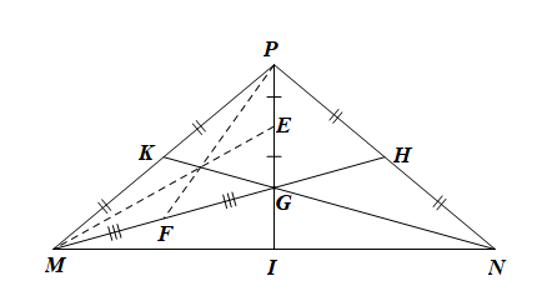
Cho tam giác MNP cân tại P. Hai đường trung tuyến MH và NK cắt nhau tại G. Kéo dài PG cắt (ảnh 1)

Xét DMNP có hai đường trung tuyến MH và NK cắt nhau tại G nên G là trọng tâm tam giác MNP. Do đó khẳng định (III) là đúng.

G là trọng tâm tam giác MNP nên PI là đường trung tuyến của tam giác.

Suy ra I là trung điểm của MN hay MI = NI.

Xét DPIN và DPIM có

NI = MI (chứng minh trên),

PI là cạnh chung,

PN = PM (do DMNP cân tại P)

Do đó DPIN = DPIM (c.c.c) nên khẳng định (II) là đúng.

Xét DPGM có PF, GK, ME là các đường trung tuyến của tam giác nên ba đường này đồng quy tại một điểm. Do đó khẳng định (I) là đúng.

Vậy cả 3 khẳng định đều đúng, ta chọn phương án D.