Cho hình chóp S.ABCD đáy hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC và SD.
Trong các đường thẳng sau đây, đường thẳng không song song với MN là
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
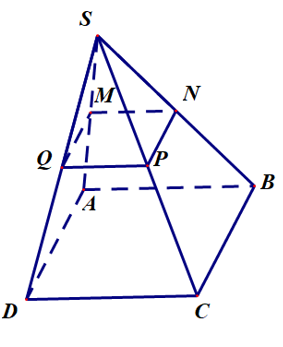
Vì M và N lần lượt là trung điểm của SA và SB nên MN là đường trung bình của tam giác SAB, từ đó suy ra MN // AB.
Tương tự suy ra PQ // CD.
Mà ABCD là hình bình hành nên CD // AB.
Vì vậy ta được MN // AB // PQ // CD.
Cho tứ diện ABCD . Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB. Hai điểm phân biệt P và Q cùng thuộc đường thẳng CD. Vị trí tương đối của hai đường thẳng MP và NQ là
Cho hình bình hành ABCD và một điểm S không nằm trên mặt phẳng (ABCD). Các điểm M, N, P, Q lần lượt là trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng không song song với MQ là
Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì
Cho hình bình hành ABCD và S không nằm trên (ABCD). Điểm N thuộc SB sao cho , M nằm trên SD sao cho . Đường thẳng song song với BD là
Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). M và N lần lượt là trung điểm của các cạnh SA và SB. Vị trí tương đối của MN và CD là
Cho 3 mặt phẳng phân biệt (M), (N), (P). Gọi , và . Khi đó ba đường thẳng a, b, c