Cho hai đường thẳng d và d’ chéo nhau và các điểm A, B, C trên d, các điểm A’, B’, C’ trên d’ sao cho . Khi đó các đường thẳng AA’, BB’, CC’
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
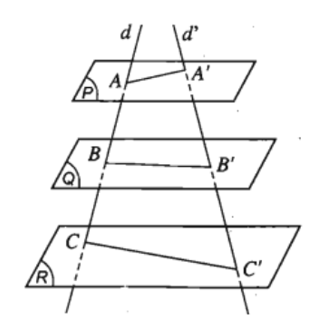
Theo định lý Thalès đảo ta có ba đường thẳng trên song song với nhau.
Cho hình chóp S.ABC, mặt phẳng (P) song song với (ABC) đi qua trọng tâm G của tam giác SAB và cắt SC tại H. Tỷ lệ bằng
Cho hình chóp S.ABC; gọi G, H là trọng tâm tam giác SAC và SBC. Gọi M là trung điểm của BC. Đường thẳng song song với (ABC) là
Hai hình vuông ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy hai điểm M và N sao cho AM = BN. Vị trí tương đối của MN và (CDFE) là
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. Trên BC lấy điểm E sao cho EB = 2EC. Vị trí tương đối của EG và (ACD) là
Cho hình chóp S.ABC. Gọi D, E, F lần lượt là trung điểm của SB, SA, SC. Vị trí tương đối của (DEF) và (ABC) là
Cho tứ diện ABCD. G là trọng tâm của tam giác ABD; M nằm trên AB sao cho AM = 2MB. Vị trí tương đối của MG và (BCD) là
Cho tứ diện ABCD. Gọi E, F là trọng tâm các tam giác ACD và ABD. Vị trí tương đối của EF và ABC là
Cho tứ diện ABCD; lấy điểm M trên cạnh AB sao cho: . Trên cạnh AC lấy điểm N sao cho MN // (BCD). Tỉ số là
Cho hình bình hành ABCD và một điểm S không nằm trên (ABCD, E và F là hai điểm trên SA; SB sao cho: . Vị trí tương đối giữa EF và (ABCD) là