Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
b) Tam giác EMC là tam giác gì?
c) Chứng minh: .
 Giải bởi Vietjack
Giải bởi Vietjack
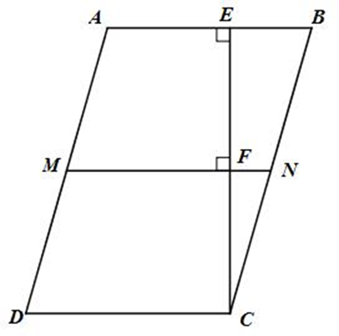
a) Ta có MN ⊥ CE (gt); AB ⊥ CE (gt)
Suy ra: MN // AB
Mà AB // CD (ABCD là hình bình hành) nên MN // CD
Tứ giác MNCD có MN // CD
Và MD // CN (AD // BC)
Do đó tứ giác MNCD là hình bình hành.
b) Gọi F là giao điểm của MN và EC
Hình thang AECD (EC // CD) có MF // AE // CD
Và M là trung điểm của AD (gt)
* F là trung điểm của EC.
ΔMEC có MF là đường trung tuyến (F là trung điểm của EC)
Và MF là đường cao
Suy ra: ΔMEC cân tại M.
c) Ta có AD = 2AB (gt)
AD = 2MD (M là trung điểm của AD)
Và AB = CD (ABCD là hình bình hành); MD = CD
Hình bình hành MNCD có MD = CD nên là hình thoi.
CM là đường phân giác nên:
Mà (hai góc so le trong và AE // MF)
Và (hai góc so le trong và MF // CD)
Nên:
Ta có: (CM là phân giác )
Và (ABCD là hình bình hành)
Vậy .
Cho tam giác ABC cân tại A, đường cao AD, K là trung điểm của AD. Gọi I là hình chiếu của điểm D trên CK. Chứng minh rằng .
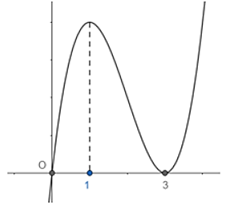
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số có đúng 3 điểm cực trị.
Cho hàm số y = x – 2 có đồ thị là đường thẳng (d).
a, Vẽ đồ thị hàm số đã cho.
b, Gọi A, B lần lượt là giao điểm của (d) với Ox, Oy. Tính diện tích tam giác OAB (đơn vị đo trên các trục tọa độ centimet).
c, Tìm giá trị của m để đường thẳng (d) và đường thẳng (d1): y = -2x + m² - 3 cắt nhau tại một điểm trên trục tung.
Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD.
Tìm giao tuyến của hai mặt phẳng
a) (SBM) và (SCD);
b) (ABM) và (SCD);
c) (ABM) và (SAC).
Cho đa thức P(x) với các hệ số nguyên thỏa mãn P(2021).P(2022) = 2023.
Chứng minh rằng đa thức P(x) - 2024 không có nghiệm nguyên.
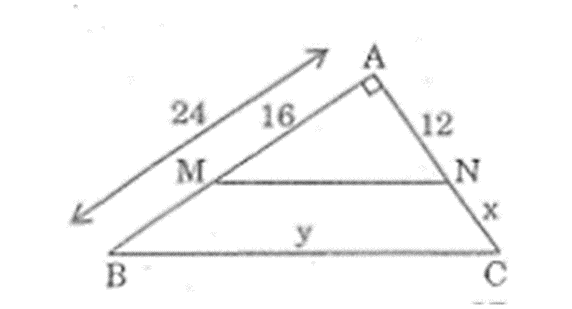
Hình vẽ cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC, BC.
Cho hình bình hành ABCD có ; AD = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD.
a) MCND là hình thoi.
b) ABMD là hình thang cân.
Cho góc nhọn xOy. Trên cạnh Ox lấy hai điểm A, B sao cho A nằm giữa O và B. Trên cạnh Oy lấy hai điểm C, D sao cho C nằm giữa O và D.
Chứng minh rằng: AB + CD < AD + BC.
Cho 2 tập hợp M = [2m − 1; 2m + 5] và N = [m + 1; m + 7] (với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.
Cho dãy số 1,1; 2,2; 3,3; …; 108,9; 110,0
a) Dãy số có bao nhiêu số hạng?
b) Số hạng thứ 30 của dãy là bao nhiêu?
Cho hình chóp S.ABCD . Gọi M, N lần lượt là trung điểm của SB và SD. Thiết diện của hình chóp S.ABCD và mặt phẳng (AMN) là hình gì?
Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của AB và CD. Gọi M, N là giao điểm của AI, CK với BD. Chứng minh: ∆ADM = ∆CBN.
Cho hình chóp S.ABCD. M là một điểm trên cạnh SC.
a) Tìm giao điểm của AM và (SBD).
b) Gọi N là một điểm trên cạnh BC. Tìm giao điểm của SD và (AMN).
Cho cấp số cộng (un) và gọi Sn là tổng n số hạng đầu tiên của nó. Biết S7 = 77, S12 = 192. Tìm số hạng tổng quát un của cấp số cộng đó?
Cho đường tròn tâm O. Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng:
a) Hai cung nhỏ CF và BD bằng nhau.
b) Hai cung nhỏ BF và DE bằng nhau.
c) DE = BF.