Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho . Điểm M di động nằm trên BC sao cho . Tìm x sao cho độ dài của đạt giá trị nhỏ nhất.
Giải bởi Vietjack
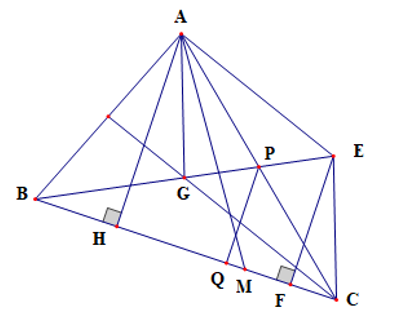
Dựng hình bình hành AGCE
Ta có:
Kẻ EF ⊥ BC (F ∈ BC)
Khi đó
Do đó đạt giá trị nhỏ nhất khi M ≡ F
Gọi P là trung điểm của AC, Q là hình chiếu vuông góc của P lên BC
Vì AGCE là hình bình hành, P là trung điểm của AC
Suy ra P là trung điểm của GE
Do đó
Vì G là trọng tâm tam giác ABC, BP là trung tuyến
Suy ra
Ta có: BE = BP + PE
Hay
Xét ∆BPQ và ∆BEF có
là góc chung;
Suy ra: ∆BPQ ∽ ∆BEF (g.g)
Do đó
Xét DAHC có P là trung điểm của AC và AH // PQ (vì cùng vuông góc với BC)
Suy ra Q là trung điểm của CH
Hay ; mà
Ta có:
Do đó:
Vậy .
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 20cm. Tính AC, BH, CH, AH?
Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm.
a) Tính HB, HC.
b) Gọi E, F lần lượt là hình chiếu của H trên AB và AC. Chứng minh AB.AC = EF.BC.
Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = 4 cm, CH = 9cm. a) Tính AH, AB, AC?
b) Gọi M là trung điểm của AC. Tính góc .
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC và M là trung điểm của BC. Chứng minh rằng:
a) EF = AH.
b) AM ⊥ EF.
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm BC, I là giao điểm của DM với AB, K là giao điểm của EM với AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân.
Cho tia Ox, vẽ hai tia Oy và Ot nằm cùng phía với đường thẳng chứa tia Ox sao cho: .
a) Tính ? Tia Oy có là tia phân giác của không? Vì sao?
b) Gọi tia Om là tia đối của tia Ox. Tính số đo của ?
c) Gọi Oz là tia phân giác của . Hỏi tia Oz có vuông góc với tia Oy không?
Cho tam giác ABC nhọn, các đường cao BD và CE. Tia phân giác của các góc ABD và ACE cắt nhau tại O, cắt AC và AB lần lượt tại N và M. Tia BN cắt CE tại K,tia CM cắt BD tại H. Chứng minh rằng:
a) BN vuông góc CM.
b) Tứ giác MNHK là hình thoi.
Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Cho tam giác ABC vuông tại A. Gọi O là trung điểm của BC. Trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Chứng minh:
a) ∆OAB = ∆ODC.
b) .
c) BC = 2 OA.
Cho tam giác ABC vuông ở A, đường cao AH. Biết AH = 6cm và BC = 13cm. Tính AB, AC.
Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN.
Cho tam giác ABC có Cạnh BC = a. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M và N. Tính theo a độ dài các đoạn thẳng DM và EN.
Cho tam giác ABC nhọn (AB < AC ) có ba đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh: tam giác AEB đồng dạng tam giác AFC.
b) Chứng minh: AF.AB = AE.AC và tam giác AEF đồng dạng với tam giác ABC.
Cho tam giác ABC vuông tại A (AB < AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC).
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NA = NB, PA = PC và tứ giác BMPN là hình bình hành.
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. Chứng minh tứ giác ABEF là hình thang cân.
Cho tứ giác lồi ABCD với hai cặp cạnh đối không song song và điểm S không nằm trong mặt phẳng chứa tứ giác. Tìm giao tuyến của các mặt phẳng (SAB) và (SCD); (SAC) và (SBD); (SAD) và (SBC).
