Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = a, DSAD đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi j là góc phẳng nhị diện [S, BC, A]. Khẳng định nào sau đây là đúng?

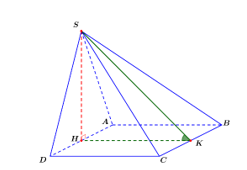
Cho hình chóp $S.ABC$, gọi $M,\,\,P$ và $I$ lần lượt là trung điểm của $AB,\,\,SC$ và $SB$. Mặt phẳng $(\alpha )$ qua $MP$ và song song với $AC$ và cắt các cạnh $SA,\,\,BC$ tại $N,\,\,Q.$

a) Chứng minh đường thẳng $BC$ song sòng với mặt phẳng $(IMP)$.

b) Xác định thiết diện của $(\alpha )$ và hình chóp. Thiết diện này là hình gì?

c) Tìm giao điểm của đường thẳng $CN$ và mặt phẳng $(SMQ)$.

Người ta trồng $3\,\,003$ cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây. Hỏi có tất cả bao nhiêu cây?

Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu $h\,{\text{(m)}}$ của mực nước trong kênh tính theo thời gian $t$ (giờ) trong một ngày $\left( {0 \leqslant t < 24} \right)$ cho bởi công thức \[h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12.\] Tìm $t$ để độ sâu của mực nước là $9\,\,{\text{m}}$ (làm tròn đến chữ số thập phân thứ hai).

Cho hình chóp $S.ABCD$ có đáy là hình thang với các cạnh đáy là $AB$ và $CD$. Gọi $I,\,\,J$ lần lượt là trung điểm của $AD$ và $BC$; $G$ là trọng tâm của tam giác $SAB.$ Giao tuyến của $(SAB)$ và $(IJG)$ là

Tìm khẳng định đúng trong các khẳng định sau.

Cho hình chóp $S.ABC$. Gọi $L,\,\,M,\,\,N$ lần lượt các điểm trên các cạnh $SA,\,\,SB$ và $AC$ sao cho $LM$ không song song với $AB,\,\,LN$ không song song với $SC$. Mặt phẳng $(LMN)$ cắt các cạnh $AB,\,\,BC,\,\,SC$ lần lượt tại $K,\,\,I,\,\,J$. Ba điểm nào sau đây thẳng hàng?

Cho tứ diện $ABCD$. Gọi $H,\,\,K$ lần lượt là trung điểm các cạnh $AB,\,\,BC.$ Trên đường thẳng $CD$ lấy điểm $M$ nằm ngoài đoạn $CD$. Thiết diện của tứ diện với mặt phẳng $(HKM)$ là

Mệnh đề nào đúng trong các mệnh đề sau?