Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), DABC là tam giác đều cạnh a, SA = 2a. Khoảng cách từ A đến mặt phẳng (SBC) bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
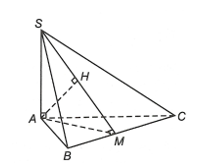
Gọi M là trung điểm BC, H là hình chiếu vuông góc của A trên SM.
Vì DABC đều nên AM ^ BC và .
Vì SA ^ (ABC) nên SA ^ BC mà AM ^ BC nên BC ^ (SAM) ⇒ BC ^ AH.
Lại có AH ^ SM do đó AH ^ (SBC) ⇒ d(A, (SBC)) = AH.
Xét DSAM vuông tại A, cóCho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, AB = a, AC = b, AD = c. Khoảng cách từ điểm A đến mặt phẳng (BCD) bằng
Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách từ A đến mặt phẳng (BCD) bằng
Cho hình chóp S.ABCD có SA ^ (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
Cho hình chóp S.ABCD có đáy là hình bình hành với . Tam giác SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB) bằng
Cho lăng trụ ABC.A'B'C' có đáy là tam giác vuông cân tại A với AB = AC = 3a. Hình chiếu vuông góc của B' lên mặt đáy là điểm H thuộc BC sao cho HC = 2HB. Biết cạnh bên của lăng trụ bằng 2a. Khoảng cách từ B đến mặt phẳng (B'AC) bằng
Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng a. Khoảng cách từ tâm của đáy đến một cạnh bên bằng
Cho tứ diện SABC trong đó SA, SB, SC vuông góc với nhau từng đôi một và SA = 3a, SB = a, SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:
Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2, BC = a. Khoảng cách từ S đến BC bằng bao nhiêu?
Cho hình chóp A.BCD có cạnh AC ^ (BCD) và BCD là tam giác đều cạnh bằng a. Biết và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng