Dạng 1: Khoảng cách từ một điểm tới một đường thẳng, mặt phẳng có đáp án
-
229 lượt thi
-
10 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), DABC là tam giác đều cạnh a, SA = 2a. Khoảng cách từ A đến mặt phẳng (SBC) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
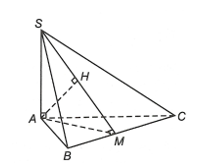
Gọi M là trung điểm BC, H là hình chiếu vuông góc của A trên SM.
Vì DABC đều nên AM ^ BC và .
Vì SA ^ (ABC) nên SA ^ BC mà AM ^ BC nên BC ^ (SAM) ⇒ BC ^ AH.
Lại có AH ^ SM do đó AH ^ (SBC) ⇒ d(A, (SBC)) = AH.
Xét DSAM vuông tại A, cóCâu 2:
Cho hình chóp S.ABCD có đáy là hình bình hành với . Tam giác SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
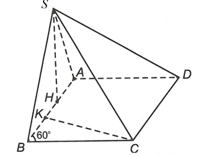
Dựng SH ^ AB. Do (SAB) ^ (ABCD) và (SAB) Ç (ABCD) = AB nên SH ^ (ABCD).
Dựng CK ^ AB.
Vì SH ^ (ABCD) ⇒ SH ^ CK mà CK ^ AB nên CK ^ (SAB).
Do CD // AB nên d(D, (SAB)) = d(C, (SAB)) = CK.
Xét DCKB vuông tại K, có CK = BC.sin60° = .
Câu 3:
Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách từ A đến mặt phẳng (BCD) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
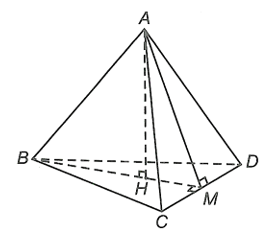
Gọi M là trung điểm CD và H là hình chiếu vuông góc của A trên BM.
Vì DBCD, DACD đều nên BM ^ CD, AM ^ CD.
Do đó CD ^ (ABM) ⇒ CD ^ AH.
Vì AH ^ BM và AH ^ CD nên AH ^ (BCD).
Do đó d(A, (BCD)) = AH.
Mà ABCD là tứ diện đều nên H là trọng tâm của DBCD.
Vì DBCD, DACD đều cạnh a nên và
Xét DAHM vuông tại H, có .
Câu 4:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, AB = a, AC = b, AD = c. Khoảng cách từ điểm A đến mặt phẳng (BCD) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
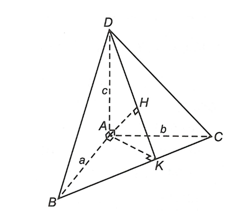
Kẻ AK ^ BC (K Î BC) và AH ^ DK (H Î DK)
Vì AD ^ AB, AD ^ AC nên AD ^ (ABC) ⇒ AD ^ BC.
Mà AK ^ BC. Do đó BC ^ (ADK) ⇒ BC ^ AH mà AH ^ DK nên AH ^ (BCD).
Do đó d(A, (BCD)) = AH.
Xét DABC vuông tại A có:
Xét DADK vuông tại A có:
Vậy
Câu 5:
Cho lăng trụ ABC.A'B'C' có đáy là tam giác vuông cân tại A với AB = AC = 3a. Hình chiếu vuông góc của B' lên mặt đáy là điểm H thuộc BC sao cho HC = 2HB. Biết cạnh bên của lăng trụ bằng 2a. Khoảng cách từ B đến mặt phẳng (B'AC) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
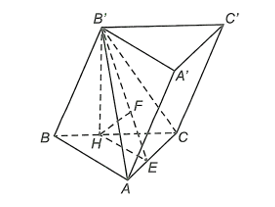
Xét DABC vuông tại A, có .
Xét DB'HB vuông tại H, có .
Kẻ HE ^ AC tại E, HF ^ B'E tại F.
Vì B'H ^ (ABC) ⇒ B'H ^ AC mà AC ^ HE nên AC ^ (B'HE) ⇒ AC ^ HF.
Mà HF ^ B'E nên HF ^ (B'AC).
Do đó d(H, (B'AC)) = HF.
Có HE // AB (vì cùng vuông góc với AC) nên .
Xét DB'HE vuông tại H, có .
Mặt khác Do đóCâu 6:
Cho hình chóp S.ABCD có SA ^ (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
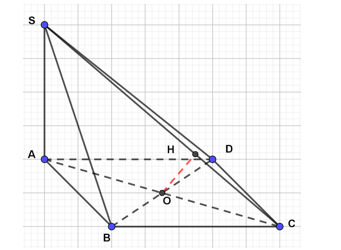
Kẻ OH ^ SC ⇒ d(O, SC) = OH.
Xét DABC vuông tại B, có .
Vì ABCD là hình vuông nên O là trung điểm của AC nên .
Xét DSAC vuông tại A, có .
Vì DCHO đồng dạng với DCAS nênCâu 7:
Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2, BC = a. Khoảng cách từ S đến BC bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
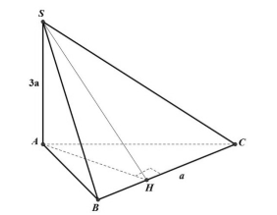
Kẻ AH ^ BC tại H .
Có .
Vì SA ^ (ABC) ⇒ SA ^ BC mà AH ^ BC ⇒ BC ^ (SAH) ⇒ BC ^ SH.
Do đó d(S, BC) = SH.
Xét DSAH vuông tại A, có .
Câu 8:
Cho hình chóp A.BCD có cạnh AC ^ (BCD) và BCD là tam giác đều cạnh bằng a. Biết và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
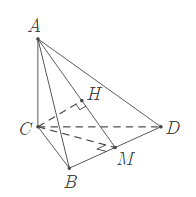
Kẻ CH ^ AM tại H. Khi đó d(C, AM) = CH.
Do DBCD đều cạnh a nên MC là đường cao và .
Vì AC ^ (BCD) nên AC ^ CM.
Xét DACM vuông tại C, ta có .Câu 9:
Cho tứ diện SABC trong đó SA, SB, SC vuông góc với nhau từng đôi một và SA = 3a, SB = a, SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
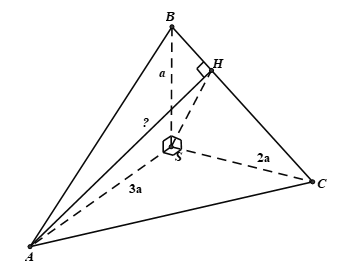
Dựng AH ^ BC tại H ⇒ d(A, BC) = AH.
Vì SA ^ SB và SA ^ SC nên SA ^ (SBC) ⇒ SA ^ BC.
Lại có AH ^ BC nên BC ^ (SAH) ⇒ BC ^ SH.
Xét DSBC vuông tại S, có .
Vì SA ^ (SBC) nên SA ^ SH.
Xét DASH vuông tại S, có .
Câu 10:
Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng a. Khoảng cách từ tâm của đáy đến một cạnh bên bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
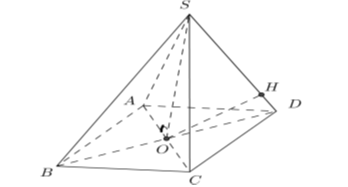
Gọi O là tâm hình vuông ABCD.
Vì S.ABCD là hình chóp đều nên SO ^ (ABCD).
Do đó hình chiếu của SD trên mặt phẳng (ABCD) là OD. Khi đó .
Kẻ OH ^ SD tại H. Khi đó d(O, SD) = OH.
Vì ABCD là hình vuông cạnh a nên mà O là trung điểm của BD nên .
Xét DOHD vuông tại H, có OH = OD.sina =
.
