Cho hình bình hành ABCD có . Tia phân giác của qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:
a) AB = 2AD.
b) DI = 2AH.
c) AC vuông góc với AD.
Giải bởi Vietjack
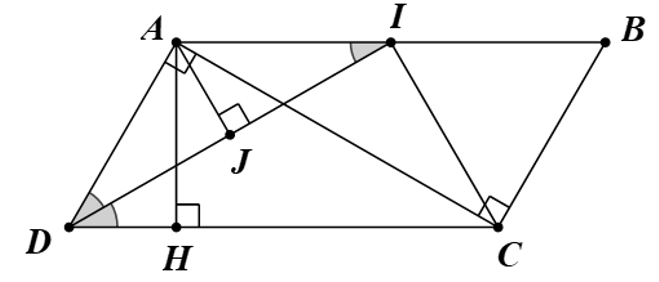
a) Hình bình hành ABCD có ở vị trí trong cùng phía.
Suy ra
Khi đó (do DI là tia phân giác của ).
Mà (cặp góc so le trong).
Vì vậy
Suy ra tam giác ADI cân tại A.
Do đó AD = AI.
Mà AB = 2AI (I là trung điểm của AB).
Vậy AB = 2AD (điều phải chứng minh).
b) Gọi J là trung điểm của DI.
Tam giác ADI có AJ là đường trung tuyến.
Suy ra AJ vừa là đường phân giác, v
Do đó ∆AJD = ∆DHA (cạnh huyền – góc nhọn).
Suy ra DJ = AH (cặp cạnh tương ứng).
Mà DI = 2DJ (J là trung điểm của DI).
Vậy DI = 2AH (điều phải chứng minh).
c) Ta có BI = BC
Suy ra tam giác IBC cân tại B.
Mà
Do đó tam giác IBC đều.
Vì vậy IC = IB = IA.
Khi đó tam giác ABC vuông tại C hay
Suy ra
Vậy AD ⊥ AC (điều phải chứng minh).
Cho tam giác ABC nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Kẻ Bx, Cy lần lượt vuông góc với AB, AC chúng cắt nhau tại K.
1. Chứng minh tứ giác BHCK là hình bình hành và H, M, K thẳng hàng
2. Gọi I là điểm đối xứng với H qua BC. Chứng minh tứ giác BIKC là hình thang cân
3. Gọi G là giao điểm của BK và HI, tam giác ABC phải có thêm điều kiện gì để tứ giác GHCK là hình thang cân.
Cho a, b, c thuộc ℕ*: a2 + b2 = c2. Chứng minh abc chia hết cho 60.
Tam giác ABC có BC = 12, CA = 9, AB = 6. Điểm M nằm trên cạnh BC sao cho BM = 4. Độ dài AM bằng bao nhiêu?
Chứng minh tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Cho 3 số nguyên tố lớn hơn 3 trong đó số sau lớn hơn số trước d đơn vị. Chứng minh rằng d chia hết cho 6.
Cho Parabol (P): y = x2 và đường thẳng (d) : y = 2(m + 3)x – 2m + 2 (m là tham số, m thuộc R).
a) Với m = - 5 tìm tọa độ giao điểm của parabol (P) và đường thẳng (d).
b) Chứng minh rằng: Parabol (P) và đường thẳng (d) cắt nhau tại hai điểm phân biệt với mọi m. Tìm m để (d) cắt (P) tại hai điểm cùng nằm bên phải trục tung.
Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho.
Cho tam giác ABC có BC = a, AC = b, AB = c. Đường trung tuyến AM = AB = c. Chứng minh rằng a2 = 2(b2 – c2)
Cho tam giác có ba cạnh lần lượt là 5,6,7. Tìm độ dài đường cao ứng với cạnh có độ dài bằng 6.
Nhà bạn Thu có một đèn trang trí có dạng hình chóp tam giác đều như Hình 10.16. Các cạnh của hình chóp đều bằng nhau và bằng 20 cm. Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu. Tính diện tích giấy bạn Thu sử dụng (coi như mép dán không đáng kể). Cho biết
Từ điểm A ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC đến (O) (B, C là các tiếp điểm).
a) Chứng minh: OA vuông góc với BC tại H.
b) Vẽ đường thẳng vuông góc với OB tại O cắt cạnh AC tại E. Chứng minh: ∆OAE là tam giác cân.
c) Trên tia đối của tia BC lấy điểm Q. Vẽ hai tiếp tuyến QM, QN đến (O) (M, N là tiếp tuyến). Chứng minh: 3 điểm A, M, N thẳng hàng.
Cho tam giác ABC có BC = a, AC = b, Ab = c, đường phân giác AD.
1. Tính độ dài BD, DC.
2. Tia phân giác của góc B cắt AD tại I. Tính tỉ số AI : ID.
3. Cho BC bằng trung bình cộng của AB và AC, gọi G là trọng tâm của tam giác ABC. Chứng minh IG song song BC.
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm.
a) Chứng minh tam giác ABC vuông.
b) Tính góc B và góc C.
Cho tam giác ABC có ; AB = 3; AC = 6. Tính độ dài đường phân giác AD?
Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết 3AB = 2AC. Tính .
b) Vẽ đường phân giác CK của tam giác AHC. Biết AH = 2,4 cm; BH = 1,8 cm. Tính CH, AC, CK, .
