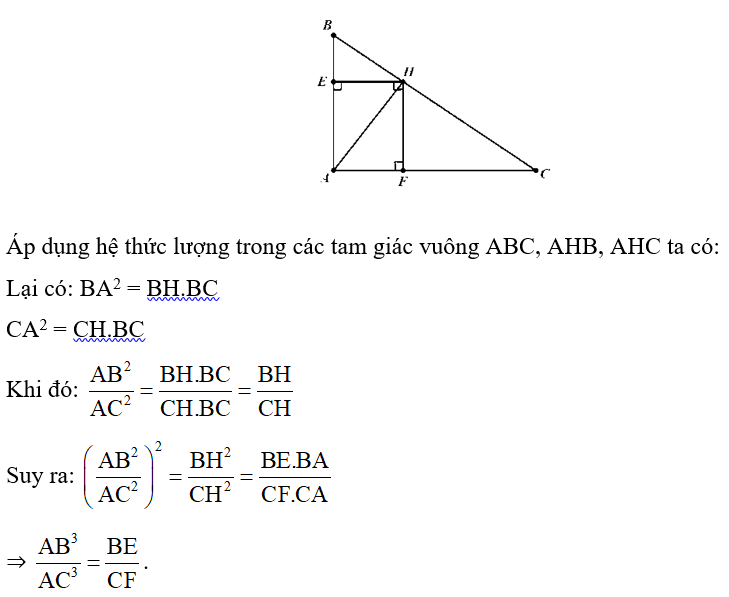
Cho tam giác ABC vuông tại A, đường cao AH kẻ HE, HF lần lượt vuông góc với AB, AC. Chứng minh .
Giải bởi Vietjack
Cho các số thực x, y thỏa mãn 4x2 + 2xy + y2 = 3.
Tìm GTLN, GTNN của P = x2 + 2xy – y2.
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O; R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC. Chứng minh AH = 2OM.
Tìm số có 2 chữ số biết rằng số đó gấp 3 lần tích các chữ số của nó.
Viết tập hợp các số tự nhiên có hai chữ số, trong đó:
a) Chữ số hàng chục nhỏ hơn chữ số hàng đơn vị là 5.
b) Chữ số hàng chục gấp bốn lần chữ số hàng đơn vị.
c) Chữ số hàng chục nhỏ hơn chữ số hàng đơn vị, tổng hai chữ số bằng 14.
Ba khối 6, 7 và 8 lần lượt có 234 học sinh, 264 học sinh và 252 học sinh xếp thành các hàng dọc để diễu hành sao cho số hàng dọc của mỗi khối như nhau. Có thể xếp nhiều nhất thành mấy hàng dọc để mỗi khối không có ai đứng lẻ hàng? Khi đó ở mỗi hàng dọc mỗi khối có bao nhiêu học sinh?
Cho hình bình hành ABCD điểm E thuộc AB, tia DE cắt tia CB tại F. Gọi G là giao điểm DE và AC. Chứng minh rằng .
Để đánh số trang của một quyển sách dày 250 trang người ta phải dùng tất cả bao nhiêu chữ số?
Cho 6 số tự nhiên khác nhau có tổng bằng 50. Chứng minh rằng trong 6 số đó tồn tại 3 số có tổng lớn hơn hoặc bằng 30.
Cho tam giác ABC thỏa mãn . Tính các góc của tam giác và bán kính đường tròn ngoại tiếp tam giác biết .
Bạn nam cùng nhóm đi mua bánh. Các bạn vào hai cửa hàng A và B thì thấy giá một cái bánh ở cả hai cửa hàng đều là 8000 đồng nhưng mỗi cửa hàng có hình thức khuyến mãi khác nhau như sau:
Cửa hàng A có chương trình khuyến mãi như sau mua 5 cái bánh được tặng thêm 1 cái bánh miễn phí.
Cửa hàng B thì giảm giá 15% cho mỗi cái bánh nếu khách hàng mua từ 4 cái trở lên. Bạn Nam và nhóm muốn mua 14 cái bánh thì nên chọn cửa hàng nào có lợi hơn?
Giả sử a, b là 2 số thực phân biệt thỏa mãn a2 + 3a = b2 + 3b = 2. Chứng minh rằng:
a) a + b = – 3.
b) a3 + b3 = – 45.
Cho dãy số 1, 4, 9, 16, 25, 36. Viết tập hợp M và chỉ ra tính chất đặc trưng.
