Chị Hà gửi vào ngân hàng \(20\,\,000\,\,000\) đồng với lãi suất \[0,5\% \]/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau \[1\] năm chị Hà nhận được bao nhiêu tiền, biết trong \[1\] năm đó chị Hà không rút tiền lần nào và lãi suất không thay đổi (làm tròn đến hàng nghìn).

Một đội văn nghệ có 4 học sinh nam và 5 học sinh nữ. Tính xác suất chọn ra một đội tốp ca gồm 3 học sinh sao cho có cả nam và nữ cùng tham gia.

Với \(a\) là số thực dương tùy ý, \(\sqrt {{a^3}} \) bằng kết quả nào sau đây?

Cho hình chóp \[S.ABCD\] có tất cả các cạnh đều bằng \(a\). Gọi \(I\) và \(J\) lần lượt là trung điểm của \(SC\) và \(BC\). Số đo của góc giữa hai đường thẳng \(IJ\) và \(CD\) bằng

Tìm hiểu thời gian chạy cự li 1000 m (đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:

Thời gian (giây) chạy trung bình cự li 1000 m của các bạn học sinh là

Cho hai biến cố \(A\) và \[B\] độc lập với nhau. Phát biểu nào sau đây là đúng?

Ông A vay dài hạn ngân hàng 300 triệu đồng, với lãi suất 12% năm. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một năm kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ liên tiếp cách nhau đúng một năm, số tiền hoàn ở mỗi lần là như nhau và trả hết nợ sau đúng 4 năm kể từ ngày vay. Hỏi theo cách đó, số tiền \(m\) mà ông A sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ.

Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số từ 1 đến 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố \(A\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố \(B\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”. Biến cố giao của hai biến cố \(A\) và \(B\) được phát biểu là:

Với \(a\) là số thực dương tùy ý, \({\log _3}\left( {9a} \right)\) bằng

Với các số thực dương \[a,b\] bất kỳ, mệnh đề nào dưới đây đúng?

Hàm số nào dưới đây là hàm số mũ?

Cho ba số thực dương \(a,b,c\) khác \(1\). Đồ thị các hàm số \(y = {a^x},y = {b^x},y = {c^x}\) được cho trong hình vẽ sau.

Mệnh đề nào dưới đây đúng?

Cho tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc với nhau (tham khảo hình vẽ).

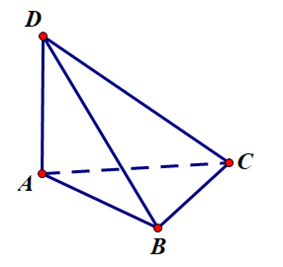
Khẳng định nào sau đây là đúng?

Cho hình lập phương \(ABCD.A'B'C'D'\) (tham khảo hình vẽ).

Góc nhị diện \(\left( {D,BC,D'} \right)\) có số đo bằng

Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Giá trị đại diện của nhóm \(\left[ {60;80} \right)\) là

Với \(\alpha \) là số thực bất kì, mệnh đề nào sau đây sai?