Đề kiểm tra Giữa kì 2 Toán 11 Cánh Diều có đáp án - Đề 01
-
229 lượt thi
-
38 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Giá trị đại diện của nhóm \(\left[ {60;80} \right)\) là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 2:
Tìm hiểu thời gian chạy cự li 1000 m (đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:

Thời gian (giây) chạy trung bình cự li 1000 m của các bạn học sinh là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 4:
Cho hai biến cố \(A\) và \(B\). Biến cố hợp của \(A\) và \(B\) có thể phát biểu dưới dạng mệnh đề nêu sự kiện là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 5:
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số từ 1 đến 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố \(A\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố \(B\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”. Biến cố giao của hai biến cố \(A\) và \(B\) được phát biểu là:
 Xem đáp án
Xem đáp án
Đáp án D
Câu 6:
Cho hai biến cố \(A\) và \[B\]. Ta có \(A\) và \[B\] được gọi là hai biến cố xung khắc khi
 Xem đáp án
Xem đáp án
Đáp án D
Câu 7:
Cho hai biến cố \(A\) và \[B\] độc lập với nhau. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 8:
Một đội văn nghệ có 4 học sinh nam và 5 học sinh nữ. Tính xác suất chọn ra một đội tốp ca gồm 3 học sinh sao cho có cả nam và nữ cùng tham gia.
 Xem đáp án
Xem đáp án
Đáp án A
Câu 9:
Cho \(A\) và \(B\) là hai biến cố độc lập với nhau, biết \(P\left( A \right) = 0,4\); \(P\left( B \right) = 0,3\). Khi đó \(P\left( {AB} \right)\) bằng
 Xem đáp án
Xem đáp án
Đáp án D
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án D
Câu 11:
Với \(a\) là số thực dương tùy ý, \(\sqrt {{a^3}} \) bằng kết quả nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 13:
Chị Hà gửi vào ngân hàng \(20\,\,000\,\,000\) đồng với lãi suất \[0,5\% \]/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau \[1\] năm chị Hà nhận được bao nhiêu tiền, biết trong \[1\] năm đó chị Hà không rút tiền lần nào và lãi suất không thay đổi (làm tròn đến hàng nghìn).
 Xem đáp án
Xem đáp án
Đáp án C
Câu 14:
Cho đẳng thức \(\frac{{\sqrt[3]{{{a^2}\sqrt a }}}}{{{a^3}}} = {a^\alpha },0 < a \ne 1.\) Khi đó \[\alpha \] thuộc khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 15:
Với điều kiện nào của \(a,\,b\) thì khẳng định \({\log _a}b = \alpha \Leftrightarrow {a^\alpha } = b\) là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Câu 19:
Cho \[\log 3 = a,\,\,\log 2 = b\]. Khi đó giá trị của \[{\log _{125}}30\] được tính theo \(a\) là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 23:
Cho ba số thực dương \(a,b,c\) khác \(1\). Đồ thị các hàm số \(y = {a^x},y = {b^x},y = {c^x}\) được cho trong hình vẽ sau.
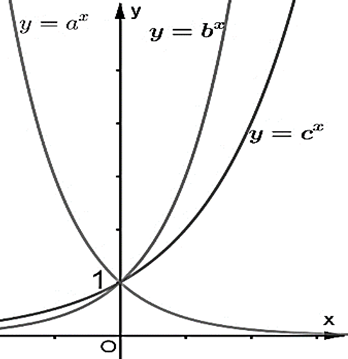
Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 24:
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
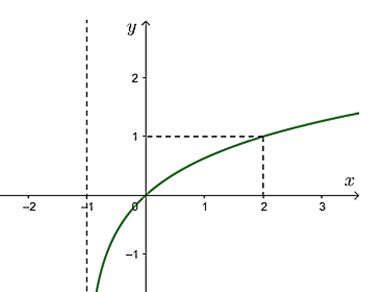
 Xem đáp án
Xem đáp án
Đáp án D
Câu 25:
Trong không gian cho hai đường thẳng thẳng \(m\) và \(n\). Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Câu 26:
Trong không gian, cho hai đường thẳng \(a\) và \(b\). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 28:
Trong không gian cho đường thẳng \(d\) vuông góc với mọi đường thẳng \(a\) nằm trong mặt phẳng \(\left( \alpha \right)\). Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 29:
Cho tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc với nhau (tham khảo hình vẽ).
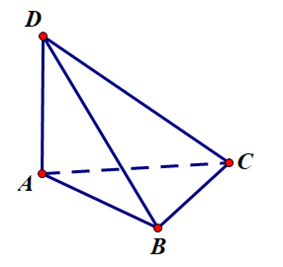
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 30:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(SB\) (tham khảo hình vẽ).
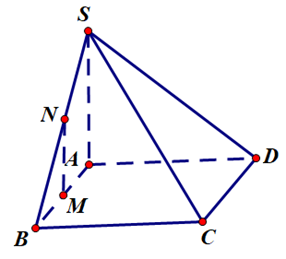
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 31:
Cho hình chóp \(S.ABCD\) có đáy là hình vuông, \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(H\) là hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {SBC} \right)\).
Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Câu 32:
Cho góc nhị diện \(\left[ {P,\,\,d,\,\,Q} \right]\) có số đo là \(\alpha \). Khi đó \(\alpha \) thỏa mãn
 Xem đáp án
Xem đáp án
Đáp án C
Câu 33:
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, \(SA \bot \left( {ABCD} \right)\). Khi đó góc giữa \(SB\) với mặt đáy là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 34:
Cho hình lập phương \(ABCD.A'B'C'D'\) (tham khảo hình vẽ).
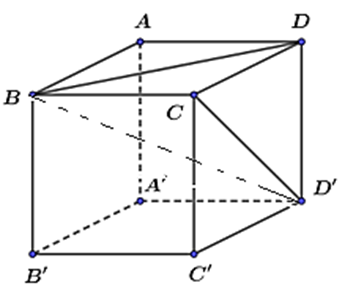
Góc nhị diện \(\left( {D,BC,D'} \right)\) có số đo bằng
 Xem đáp án
Xem đáp án
Đáp án A
Câu 35:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a\sqrt 2 ,\,AD = a\), \(SA\) vuông góc với đáy và \(SA = a\) (tham khảo hình vẽ).
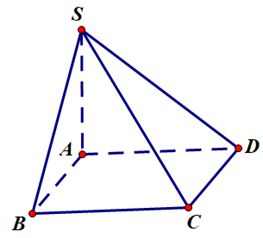
Góc giữa \(SC\) với mặt phẳng \(\left( {SAB} \right)\) bằng
 Xem đáp án
Xem đáp án
Đáp án D
Câu 36:
a) Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một số học sinh thu được kết quả sau:

Hãy cho biết ngưỡng thời gian để xác định 25% học sinh hoàn thành bài tập với thời gian lâu nhất.
b) Cho \[a,b > 0\] và \[a,b \ne 1\], thu gọn biểu thức sau
\[Q = {\log _{{a^2}}}\left( {{a^{10}}{b^2}} \right) + {\log _{\sqrt a }}\left( {\frac{a}{{\sqrt b }}} \right) + {\log _{\sqrt[3]{b}}}{b^{ - 2}}\].
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Cỡ mẫu: \(n = 2 + 4 + 7 + 4 + 3 = 20\).
Gọi \({x_1},\,{x_2},\,...,{x_{20}}\) là thời gian hoàn thành bài tập của 20 học sinh được điều tra và giả sử dãy này đã được sắp xếp theo thứ tự không giảm.
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{15}} + {x_{16}}}}{2}\). Do \({x_{15}},\,\,{x_{16}}\) đều thuộc nhóm \(\left[ {12;16} \right)\) nên nhóm này chứa \({Q_3}\).
Do đó: \(p = 4\), \({a_4} = 12\), \({m_4} = 4\), \({m_1} + {m_2} + {m_3} = 2 + 4 + 7 = 13\), \({a_5} - {a_4} = 4\). Ta có:
\({Q_3} = 12 + \frac{{\frac{{3.20}}{4} - 13}}{4}.4 = 14\).
Vậy ngưỡng thời gian cần tìm là 14 phút.
b) \[Q = {\log _{{a^2}}}\left( {{a^{10}}{b^2}} \right) + {\log _{\sqrt a }}\left( {\frac{a}{{\sqrt b }}} \right) + {\log _{\sqrt[3]{b}}}{b^{ - 2}}\]
\[ = \frac{1}{2}\left[ {{{\log }_a}{a^{10}} + {{\log }_a}{b^2}} \right] + 2\left[ {{{\log }_a}a - {{\log }_a}\sqrt b } \right] + 3 \cdot \left( { - 2} \right){\log _b}b\] \[ = \frac{1}{2}\left[ {10 + 2{{\log }_a}b} \right] + 2\left[ {1 - \frac{1}{2}{{\log }_a}b} \right] - 6 = 1.\]
Câu 37:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật tâm \[O\], \[SA\] vuông góc với mặt phẳng đáy.
a) Chứng minh \[AD \bot \left( {SAB} \right)\].
b) Tính số đo góc của góc nhị diện \(\left[ {B,SA,D} \right]\).
 Xem đáp án
Xem đáp án
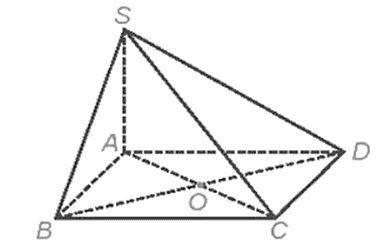
a) Vì \(SA\) vuông góc với mặt phẳng \[ABCD\] nên suy ra \(SA \bot AD\).
Theo đề bài đáy \[ABCD\] là hình chữ nhật nên \(AB \bot AD\).
Vì \(AD\) vuông góc với hai đường thẳng \(SA\) và \(AB\) nên \(AD \bot \left( {SAB} \right)\) .
b) Vì \(SA \bot \left( {ABCD} \right)\) nên \(AB\) và \(AD\) cùng vuông góc với \(SA\). Vậy \(\widehat {BAD}\) là một góc phẳng của góc nhị diện \(\left[ {B,SA,D} \right]\).
Vì \(ABCD\) là hình chữ nhật nên \(\widehat {BAD} = 90^\circ \).
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \(90^\circ \).
Câu 38:
Ông A vay dài hạn ngân hàng 300 triệu đồng, với lãi suất 12% năm. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một năm kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ liên tiếp cách nhau đúng một năm, số tiền hoàn ở mỗi lần là như nhau và trả hết nợ sau đúng 4 năm kể từ ngày vay. Hỏi theo cách đó, số tiền \(m\) mà ông A sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Số tiền nợ sau năm thứ nhất:
\[{T_1} = 300\left( {1 + 12\% } \right) - m = 300p - m\], với \[p = 1 + 12\% = 1,12\].
Số tiền nợ sau năm thứ hai:
\[{T_2} = \left( {300p - m} \right)p - m = 300{p^2} - mp - m\].
Số tiền nợ sau năm thứ ba:
\[{T_3} = \left( {300{p^2} - mp - m} \right)p - m = 300{p^3} - m{p^2} - mp - m\]
Trả hết nợ sau năm thứ tư: \[\left( {300{p^3} - m{p^2} - mp - m} \right)p - m = 0\]
\[ \Leftrightarrow 300{p^4} - m{p^3} - m{p^2} - mp - m = 0 \Leftrightarrow 300{p^4} - m\left( {{p^3} + {p^2} + p + 1} \right) = 0\]
\[ \Leftrightarrow 300{p^4} - m \cdot \frac{{\left( {{p^4} - 1} \right)}}{{p - 1}} = 0 \Leftrightarrow 300 \cdot {\left( {1,12} \right)^4} = m \cdot \frac{{\left[ {{{\left( {1,12} \right)}^4} - 1} \right]}}{{0,12}}\]
\[ \Leftrightarrow m = \frac{{300 \cdot {{\left( {1,12} \right)}^4} \cdot \left( {0,12} \right)}}{{{{\left( {1,12} \right)}^4} - 1}} \Leftrightarrow m = \frac{{36 \cdot {{\left( {1,12} \right)}^4}}}{{{{\left( {1,12} \right)}^4} - 1}}\].
Vậy \[m = \frac{{36 \cdot {{\left( {1,12} \right)}^4}}}{{{{\left( {1,12} \right)}^4} - 1}} \approx 98,77\] triệu đồng.
