Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
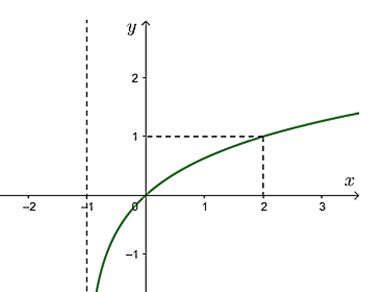
B. \[y = {\log _2}\left( {x + 1} \right)\].
D. \(y = {\log _3}\left( {x + 1} \right)\).
Giải bởi Vietjack
Đáp án D
Một đội văn nghệ có 4 học sinh nam và 5 học sinh nữ. Tính xác suất chọn ra một đội tốp ca gồm 3 học sinh sao cho có cả nam và nữ cùng tham gia.
Cho góc nhị diện \(\left[ {P,\,\,d,\,\,Q} \right]\) có số đo là \(\alpha \). Khi đó \(\alpha \) thỏa mãn
Tìm hiểu thời gian chạy cự li 1000 m (đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:
Thời gian (giây) chạy trung bình cự li 1000 m của các bạn học sinh là
Với \(a\) là số thực dương tùy ý, \(\sqrt {{a^3}} \) bằng kết quả nào sau đây?
Với điều kiện nào của \(a,\,b\) thì khẳng định \({\log _a}b = \alpha \Leftrightarrow {a^\alpha } = b\) là đúng?
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số từ 1 đến 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố \(A\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố \(B\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”. Biến cố giao của hai biến cố \(A\) và \(B\) được phát biểu là:
Với \(a\) là số thực dương tùy ý, \({\log _3}\left( {9a} \right)\) bằng
Cho hai biến cố \(A\) và \[B\]. Ta có \(A\) và \[B\] được gọi là hai biến cố xung khắc khi
Cho hai biến cố \(A\) và \[B\] độc lập với nhau. Phát biểu nào sau đây là đúng?
Cho tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc với nhau (tham khảo hình vẽ).
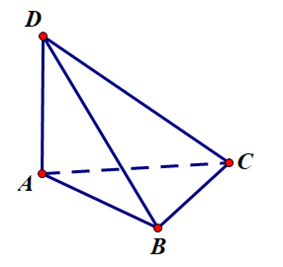
Khẳng định nào sau đây là đúng?
a) Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một số học sinh thu được kết quả sau:
Hãy cho biết ngưỡng thời gian để xác định 25% học sinh hoàn thành bài tập với thời gian lâu nhất.
b) Cho \[a,b > 0\] và \[a,b \ne 1\], thu gọn biểu thức sau
\[Q = {\log _{{a^2}}}\left( {{a^{10}}{b^2}} \right) + {\log _{\sqrt a }}\left( {\frac{a}{{\sqrt b }}} \right) + {\log _{\sqrt[3]{b}}}{b^{ - 2}}\].
