Cho tứ diện $ABCD$ có tam giác $ABC$ cân tại $A$, tam giác $BCD$ cân tại $D$. Gọi $I$ là trung điểm cạnh $BC$.
a) Chứng minh rằng $BC \bot \left( {AID} \right)$.
b) Gọi $AH$ là đường cao của tam giác $AID$. Chứng minh rằng $AH \bot BD$.
 Giải bởi Vietjack
Giải bởi Vietjack
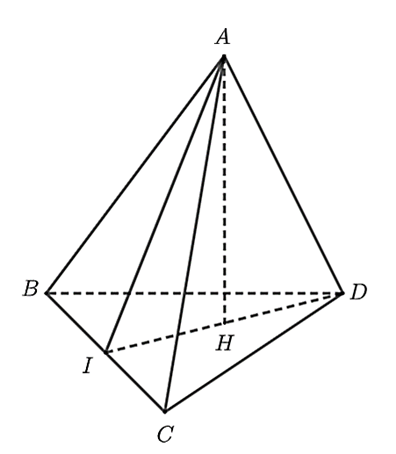
a) Vì tam giác $ABC$ cân tại $A$ có $AI$ là trung tuyến nên $AI$ đồng thời là đường cao, do đó $AI \bot BC$. (1)
Vì tam giác $BCD$ cân tại $D$ có $DI$ là trung tuyến nên $DI$ đồng thời là đường cao, do đó $DI \bot BC$. (2)
Từ (1) và (2) suy ra $BC \bot \left( {AID} \right)$.
b) Vì $AH$ là đường cao của tam giác $AID$ nên $AH \bot ID$.
Lại có $BC \bot \left( {AID} \right)$ nên $BC \bot AH$.
Ta có $\left\{ \begin{gathered}
AH \bot ID \hfill \\
AH \bot BC \hfill \\
ID,\,BC \subset \left( {BCD} \right) \hfill \\
ID \cap BC = I \hfill \\
\end{gathered} \right. \Rightarrow AH \bot \left( {BCD} \right)$.
Từ đó suy ra $AH \bot BD$.
Cho hình lập phương $ABCD.A'B'C'D'$ (như hình vẽ dưới).
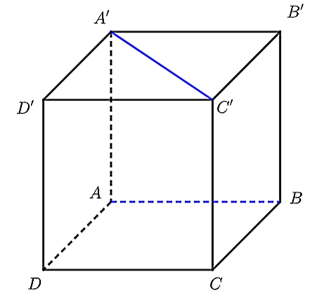
Góc giữa hai đường thẳng $AB$ và $A'C'$ bằng
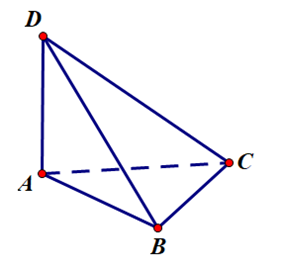
Khẳng định nào sau đây là đúng?
Cho hình lập phương $ABCD.A'B'C'D'$ (như hình vẽ dưới).
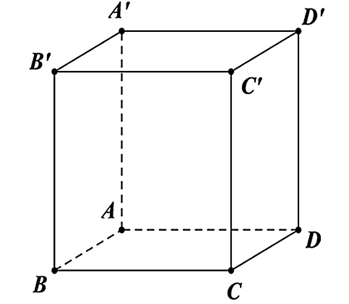
Đường thẳng nào sau đây vuông góc với đường thẳng $BC'$?
Cho hình chóp $S.ABCD$ có đáy là hình vuông, $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Gọi $H$ là hình chiếu vuông góc của $A$ lên mặt phẳng $\left( {SBC} \right)$.
Khẳng định nào sau đây là khẳng định đúng?
Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, $SA$ vuông góc với đáy (tham khảo hình vẽ).
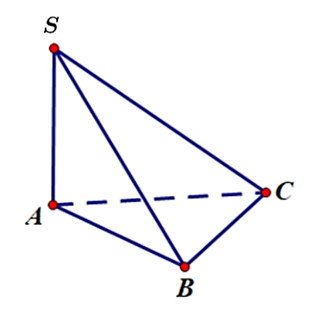
Khẳng định nào sau đây sai?
Với $a$ là số thực dương tùy ý, $\sqrt {{a^3}} $ bằng kết quả nào sau đây?
Trong không gian cho hai đường thẳng thẳng $m$ và $n$. Phát biểu nào sau đây là đúng?
Trong không gian, cho hai đường thẳng $a$ và $b$. Khẳng định nào sau đây là đúng?
Trong không gian cho đường thẳng $d$ vuông góc với mọi đường thẳng $a$ nằm trong mặt phẳng $\left( \alpha \right)$. Khẳng định nào sau đây đúng?
a) Tính giá trị của biểu thức $M = {\left( {3 + 2\sqrt 2 } \right)^{2019}} \cdot {\left( {3\sqrt 2 - 4} \right)^{2018}}$.
b) Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \log \left( {{x^2} - 2mx + 4} \right)$ có tập xác định là $\mathbb{R}$.
Với điều kiện nào của $a,\,b$ thì khẳng định ${\log _a}b = \alpha \Leftrightarrow {a^\alpha } = b$ là đúng?