Điểm $M$ trên đường tròn lượng giác dưới đây biểu diễn cho góc lượng giác nào trong các đáp án A, B, C, D?
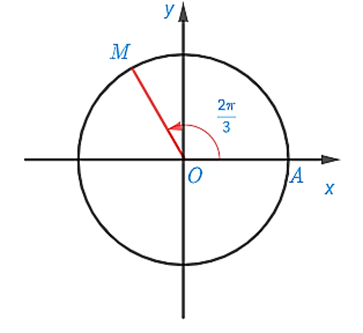
D. $ - \frac{{5\pi }}{3}$
Giải bởi Vietjack
Chọn B
Cho 2 cấp số cộng hữu hạn, mỗi cấp số cộng có 100 số hạng: \[4,7,10,13,16,...\] và \[1,6,11,16,21,...\]. Hỏi có tất cả bao nhiêu số có mặt trong cả 2 cấp số trên.
Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = 24$ và $\frac{{{u_4}}}{{{u_{11}}}} = 16384$. Số hạng ${u_{17}}$ là
Cho dãy số $\left( {{u_n}} \right)$ với \[{u_n} = \frac{3}{2}{.5^n}\]. Khẳng định nào sau đây là đúng?
Cho \[\tan \alpha = - \frac{4}{5}\] với \[\frac{{{\text{3}}\pi }}{{\text{2}}} < \alpha < 2\pi \]. Khi đó
Trung vị của mẫu số liệu ghép nhóm trên Câu 34 gần nhất với giá trị nào dưới đây.
Cho mẫu số liệu ghép nhóm sau:
|
Nhóm |
$\left[ {0;2} \right)$ |
$\left[ {2;4} \right)$ |
$\left[ {4;6} \right)$ |
$\left[ {6;8} \right)$ |
$\left[ {8;10} \right)$ |
$\left[ {10;12} \right)$ |
$\left[ {12;14} \right)$ |
|
Tần số |
5 |
10 |
40 |
20 |
16 |
3 |
6 |
Mệnh đề nào dưới đây là đúng?
Biểu thức \[A = \frac{{2{{\cos }^2}2\alpha + \sqrt 3 \sin 4\alpha - 1}}{{2{{\sin }^2}2\alpha + \sqrt 3 \sin 4\alpha - 1}}\] có kết quả rút gọn là
Giả sử các đẳng thức đều có nghĩa. Đẳng thức sai trong các đẳng thức sau là
Hàm số $y = A\sin \omega t$ $\left( {\omega \ne 0} \right)$ là hàm số tuần hoàn với chu kì
Cho cấp số cộng $\left( {{u_n}} \right)$ biết ${u_5} = 18$ và $4{S_n} = {S_{2n}}$. Số hạng đầu ${u_1}$ và công sai $d$ là
Phép biến đổi nào trong các phép biến đổi sau đây không phải là phép biến đổi tương đương?
Cho dãy số $\left( {{u_n}} \right)$ có ${u_n} = \frac{{2n}}{{{n^2} + 1}}$. Số $\frac{9}{{41}}$ là số hạng thứ bao nhiêu của dãy số $\left( {{u_n}} \right)$?
độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây?
. Tính tổng 
, trong đó a là tham số thực. Tìm a để 
bằng:
là:
là:
bằng
bằng