Trong không gian \[Oxyz,\] cho hai điểm \[A\left( {3\,;\,\,1\,;\,\,2} \right),\,\,B\left( { - 3\,;\,\, - 1\,;\,\,0} \right)\] và mặt phẳng \((P):x + y + 3z - 14 = 0.\) Điểm \(M\) thuộc mặt phẳng \((P)\) sao cho \(\Delta MAB\) vuông tại \[M.\] Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {Oxy} \right).\)
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi toạ độ của điểm \(M\) là \[M\left( {x\,;\,\,y\,;\,\,z} \right)\]
\( \Rightarrow \overrightarrow {AM} = \left( {x - 3\,;\,\,y - 1\,;\,\,z - 2} \right),\,\,\overrightarrow {BM} = \left( {x + 3\,;\,\,y + 1\,;\,\,z} \right){\rm{.}}\)
Vì \(\Delta MAB\) vuông tại \(M\) nên \(\overrightarrow {AM} \cdot \overrightarrow {BM} = 0 \Leftrightarrow \left( {x - 3} \right)\left( {x + 3} \right) + \left( {y - 1} \right)\left( {y + 1} \right) + z\left( {z - 2} \right) = 0\)
\( \Leftrightarrow {x^2} - 9 + {y^2} - 1 + {z^2} - 2z = 0 \Leftrightarrow {x^2} + {y^2} + {\left( {z - 1} \right)^2} = 11.{\rm{ }}\)
\( \Rightarrow M\) thuộc mặt cầu \((S)\) có tâm \(I\left( {0\,;\,\,0\,;\,\,1} \right)\) và bán kính \(R = \sqrt {11} .\)
Ta có \(d\left( {I,\,\,\left( P \right)} \right) = \frac{{\left| {0 + 0 + 3 \cdot 1 - 14} \right|}}{{\sqrt {{1^2} + {1^2} + {3^3}} }} = \sqrt {11} = R\)\( \Rightarrow (P)\) tiếp xúc với \((S)\) tại \(M\)
\( \Rightarrow IM \bot (P)\) hay \(M\) là hình chiếu vuông góc của \(I\) trên \((P)\)
Ta có \(M \in (P) \Rightarrow x + y + 3z = 14\) (1).
\(\overrightarrow {IM} = \left( {x\,;\,\,y\,;\,\,z - 1} \right)\) cùng phương với VTPT của mặt phẳng \((P) \Rightarrow \frac{x}{1} = \frac{y}{1} = \frac{{z - 1}}{3}\)
Từ (1) và (2) ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y + 3z = 14}\\{\frac{x}{1} = \frac{y}{1} = \frac{{z - 1}}{3}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 1}\\{z = 4}\end{array} \Rightarrow M\left( {1\,;\,\,1\,;\,\,4} \right)} \right.} \right..\)
Vậy \(d\left( {M\,;\,\,\left( {Oxy} \right)} \right) = \left| 4 \right| = 4.\)
Đáp án: 4.
Trong không gian \[Oxyz,\] cho tam giác \[ABC\] có \(A\left( {1\,;\,\,2\,;\,\, - 1} \right),\,\) \(B\left( {2\,;\,\, - 1\,;\,\,3} \right),\,\)\(C\left( { - 4\,;\,\,7\,;\,\,5} \right).\) Gọi \(D\left( {a\,;\,\,b\,;\,\,c} \right)\) là chân đường phân giác trong góc \(B\) của tam giác \[ABC\]. Giá trị của \(a + b + 2c\) bằng
Cho hình chóp \[S.ABCD.\] Gọi \[I,\,\,J,\,\,K,\,\,H\] lần lượt là trung điểm các cạnh \[SA,\,\,SB,\,\,SC,\,\]\[\,SD.\] Tính thể tích khối chóp \[S.ABCD\] biết thể tích khối chóp \[S.IJKH\] bằng 1.
Cho cân bằng hóa học sau:
Cho các biện pháp:
(1) tăng nhiệt độ,
(2) tăng áp suất chung của hệ phản ứng,
(3) hạ nhiệt độ,
(4) dùng thêm chất xúc tác \({{\rm{V}}_2}{{\rm{O}}_5}\),
(5) giảm nồng độ \({\rm{S}}{{\rm{O}}_3}\),
(6) giảm áp suất chung của hệ phản ứng.
Những biện pháp nào làm cân bằng trên chuyển dịch theo chiều thuận?
Một người chơi nhảy bungee trên một cây cầu với một sợi dây dài \[100{\rm{ }}m.\] Sau mỗi lần rơi xuống, người chơi được kéo lên một quãng đường có độ dài bằng 80% so với lần rơi trước và lại rơi xuống đúng bằng quãng đường vừa được kéo lên. Tổng quãng đường đi lên của người đó sau 10 lần được kéo lên là
Trong không gian Oxyz, cho đường thẳng \(\Delta :\frac{x}{2} = \frac{y}{{ - 1}} = \frac{{z - 1}}{{ - 1}}\) và hai điểm \(A\left( { - 1\,;\,\, - 1\,;\,\,6} \right),\,\,B\left( {2\,;\,\, - 1\,;\,\,0} \right).\) Biết điểm \(M\) thuộc \(\Delta \) sao cho biểu thức \(M{A^2} + 3M{B^2}\) đạt giá trị nhỏ nhất là \({T_{\min }}.\) Khi đó giá trị của \({T_{\min }}\) bằng
Cho phương trình \({x^2} - 2mx + {m^2} - 1 = 0.\) Với giá trị nào của tham số \(m\) thì phương trình có hai nghiệm âm phân biệt?
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2021\,;\,\,2021} \right]\) để đồ thị hàm số \(y = \frac{{x + 2}}{{\sqrt {{x^2} - 2x + m} }}\) có hai đường tiệm cận đứng?
Khi thực hành thí nghiệm phản ứng của hexane \(\left( {{{\rm{C}}_6}{{\rm{H}}_{14}}} \right)\) với bromine \(\left( {{\rm{B}}{{\rm{r}}_2}} \right).\) Cần tiến hành các bước:
Bước 1: Cho vào ống nghiệm khô khoảng \(1\;{\rm{mL}}\) hexane và nhỏ thêm vào ống nghiệm khoảng \(1\;{\rm{mL}}\) nước bromine. Quan sát màu sắc sau đó lắc nhẹ hỗn hợp rồi để yên 10 phút.
Bước 2: Nút ống nghiệm bằng bông đã tẩm dung dịch \({\rm{NaOH}}\) rồi nhúng phần đáy ống nghiệm vào cốc nước nóng \({50^o }{\rm{C}}\) (đã chuẩn bị trước) hoặc để ống nghiệm ra nơi có ánh sáng Mặt Trời. Biết hexane có khối lượng riêng nhỏ hơn nước.
Chú ý an toàn: Hexane, bromine và hydrogen bromine \(({{\rm{C}}_6}{{\rm{H}}_{13}}{\rm{Br}})\) dễ bay hơi, có mùi xốc, độc. Hiện tượng quan sát được như sau:
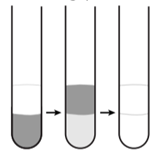
Phát biểu nào sau đây là sai?
Hằng ngày mực nước con kênh lên xuống theo thủy triều. Độ sâu \(h\) (mét) của mực nước trong kênh được tính tại thời điểm \(t\) (giờ) trong một ngày bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{8} + \frac{\pi }{4}} \right) + 12.\) Mực nước của kênh cao nhất khi \(t = {t_0}.\) Tính \(P = t_0^2 + {t_0}.\)
Tìm các giá trị của tham số \(m\) để hàm số \(y = {x^3} + \left( {3m - 1} \right){x^2} + {m^2}x - 3\) đạt cực tiểu tại \(x = - 1\)?
Cho hàm số \(f\left( x \right)\) thỏa mãn các điều kiện \(f'\left( x \right) = a{x^2} + \frac{b}{{{x^3}}},\,\,f'(1) = 3,\,\,f\left( 1 \right) = 2\) và \(f\left( {\frac{1}{2}} \right) = - \frac{1}{{12}}.\) Khi đó, giá trị của \(2a + b\) bằng