Đọc đoạn trích sau đây và trả lời câu hỏi:

Sau Tết Nguyên đán một tháng là thời gian thích nhất ở rừng. Cây cối đều nhú lộc non. Rừng xanh ngắt và ẩm ướt. Thiên nhiên vừa trang trọng, vừa tình cảm. Điều ấy một phần là do mưa xuân.

Khoảng thời gian này mà đi trong rừng, chân dẫm lên lớp lá ải mục, hít thở không khí trong lọc, thỉnh thoảng lại được thót mình bởi một giọt nước trên cây rỏ xuống vai trần thì thật tuyệt thú. Tất cả những trò nhố nhăng đê tiện vấp phải hàng ngày hoàn toàn có thể rũ sạch bởi một cú nhảy của con sóc nhỏ trên cành dâu da.

Chính dịp đó ông Diểu đi săn.

Ý nghĩ đi săn nảy sinh khi thằng con học ở nước ngoài gửi về biếu ông khẩu súng hai nòng. Khẩu súng tuyệt vời, nhẹ bỗng, hệt như một thứ đồ chơi, thật nằm mơ cũng không thấy được. ở tuổi sáu mươi, với khẩu súng mới, đi săn trong rừng vào một ngày xuân kể cũng đáng sống.

Ông Diểu nai nịt, mặc quần áo ấm, đội mũ lông và dận đôi giày cao cố. Để cho cẩn thận, ông còn mang theo cả nắm xôi nếp. Ông đi men theo suối cạn, cứ thế ngược lên mó nước đầu nguồn. Cách mó nước một dặm là vương quốc của hang động đá vôi.

(Muối của rừng – Nguyễn Huy Thiệp)

Đoạn trích được kể bởi ngôi thứ mấy?

Cho hàm số \(y = \frac{{x + 3}}{{x + 1}}\) có đồ thị \[\left( C \right)\] và đường thẳng \(d:y = x - m\), với \(m\) là tham số thực. Biết rằng đường thẳng \(d\) cắt \[\left( C \right)\] tại hai điểm phân biệt \[A\] và \[B\] sao cho điểm \(G\left( {2\,;\,\, - 2} \right)\) là trọng tâm của tam giác \[OAB\] \[(O\] là gốc tọa độ). Giá trị của \(m\) bằng

Cho hàm số \(f\left( x \right) = \frac{{ax + 1}}{{bx + c}}\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:

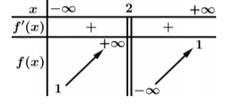
Trong các số \[a,\,\,b,\,\,c\] có bao nhiêu số dương?

Số giờ có ánh sáng mặt trời của một thành phố  ở vĩ độ \(40^\circ \) bắc trong ngày thứ \(t\) của một năm không nhuận được cho bởi một hàm số \(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365.\) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?\({\rm{A}}\)

Trong không gian với hệ tọa độ \[Oxyz,\] cho hai điểm \(A\left( {0\,;\,\,2\,;\,\, - 2} \right),\,\,B\left( {2\,;\,\,2\,;\,\, - 4} \right).\) Giả sử \[I\left( {a\,;\,\,b\,;\,\,c} \right)\] là tâm đường tròn ngoại tiếp tam giác \[OAB.\] Tính \(T = {a^2} + {b^2} + {c^2}\).

Cho hàm số \(y = f\left( x \right) = {m^2}\left( {\sqrt {2 + x}  + \sqrt {2 - x} } \right) + 4\sqrt {4 - {x^2}}  + m + 1.\) Tổng tất cả các giá trị của \(m\) để hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất bằng 4 là

Trong không gian với hệ trục tọa độ \[Oxyz,\] gọi \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) là tâm mặt cầu đi qua điểm \(A\left( {1\,;\,\, - 1\,;\,\,4} \right)\) và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính \(P = a - b + c.\)

Trong không gian \[Oxyz,\] cho mặt phẳng \((\alpha ):ax - y + 2z + b = 0\) đi qua giao tuyến của hai mặt phẳng \((P):x - y - z + 1 = 0\) và \((Q):x + 2y + z - 1 = 0.\) Giá trị của \(a + 4b\) bằng

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu \((S):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\) và hai điểm \(A\left( {4\,;\,\,3\,;\,\,1} \right),\,\,B\left( {3\,;\,\,1\,;\,\,3} \right)\,;\,\,M\) là điểm thay đổi trên \((S)\). Gọi \[m,\,\,n\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = 2M{A^2} - M{B^2}\). Tính \(m - n.\)