Một lọ đựng dung dịch \({\rm{FeS}}{{\rm{O}}_4}\)(dung dịch X) để lâu ngày thì thấy màu của dung dịch chuyển sang màu vàng nâu.
Để xác định nồng độ ban đầu của \({\rm{FeS}}{{\rm{O}}_4}\), tiến hành như sau:
Thí nghiệm 1: thêm dung dịch \({\rm{NaOH}}\) từ từ tới dư vào \(50,00\;{\rm{mL}}\) dung dịch X thấy xuất hiện kết tủa, lọc kết tủa, làm khô cẩn thận thu được 4,67 g kết tủa.
Thí nghiệm 2: thêm từ từ dung dịch \({\rm{KMn}}{{\rm{O}}_4}0,50{\rm{M}}\) trong môi trường \({{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}\) vào \(50,00\;{\rm{mL}}\) dung dịch X, sau phản ứng thấy dùng hết \(16,00\;{\rm{mL}}\) dung dịch \({\rm{KMn}}{{\rm{O}}_4}.\)
Nồng độ ban đầu của \({\rm{FeS}}{{\rm{O}}_4}\) là
A. \(1,25{\rm{M}}.\)
 Giải bởi Vietjack
Giải bởi Vietjack
Phân tích bài toán như sau:
Tại TN1: Kết tủa gồm \({\rm{Fe}}{({\rm{OH}})_2}\) và \({\rm{Fe}}{({\rm{OH}})_3}\)
\({\rm{FeS}}{{\rm{O}}_4} + 2{\rm{NaOH}} \to {\rm{Fe}}{({\rm{OH}})_2} \downarrow + {\rm{N}}{{\rm{a}}_2}{\rm{S}}{{\rm{O}}_4}\)
\({\rm{F}}{{\rm{e}}_2}{\left( {{\rm{S}}{{\rm{O}}_4}} \right)_3} + 6{\rm{NaOH}} \to 2{\rm{Fe}}{({\rm{OH}})_3} \downarrow + 3{\rm{N}}{{\rm{a}}_2}{\rm{S}}{{\rm{O}}_4}\)
Tại TN2: Chỉ có muối sắt (II) mới làm mất màu dung dịch \({\rm{KMn}}{{\rm{O}}_4}\) trong môi trường \({{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}.\)
\({n_{{\rm{KMn}}{{\rm{O}}_4}}} = 0,5 \cdot \frac{{16}}{{1000}} = {8.10^{ - 3}}\;{\rm{mol}}\)
Phương trình hóa học:
\(\begin{array}{l}10{\rm{FeS}}{{\rm{O}}_4} + 2{\rm{KMn}}{{\rm{O}}_4} + 8{{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4} \to 5{\rm{F}}{{\rm{e}}_2}{\left( {{\rm{S}}{{\rm{O}}_4}} \right)_3} + {{\rm{K}}_2}{\rm{S}}{{\rm{O}}_4} + 2{\rm{MnS}}{{\rm{O}}_4} + 8{{\rm{H}}_2}{\rm{O}}\\0,04\,\,\,\, \leftarrow {8.10^{ - 3}}\;{\rm{mol}}\end{array}\)
Þ \({{\rm{n}}_{{\rm{FeS}}{{\rm{O}}_4}}} = 0,04\) mol \( \Rightarrow {n_{Fe{{(OH)}_2}\,\,(TN1)}} = {n_{FeS{O_4}}} = 0,04\,mol\)
Ở TN1, thu được 4,67 gam kết tủa nên ta có:
4,67 = 0,04.90 + \({n_{Fe{{(OH)}_3}}} \cdot 107 \Rightarrow {n_{Fe{{(OH)}_3}}} = 0,01\,mol\)
Bảo toàn nguyên tố \(({\rm{Fe}})\) ta có:
Nồng độ ban đầu của \({\rm{FeS}}{{\rm{O}}_4}\) là \( = \frac{{0,05}}{{0,05}} = 1M\)
Chọn C.
Một xe khách đi từ Việt Trì về Hà Nội chở tối đa 60 hành khách một chuyến. Nếu một chuyến chở được \(m\) hành khách thì giá tiền cho mỗi hành khách được tính là \({\left( {30 - \frac{{5m}}{2}} \right)^2}\) đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận của mỗi chuyến xe là lớn nhất.
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left( {x + 1} \right)\left( {x - 3} \right) + \sqrt {8 + 2x - {x^2}} = 2m\) có nghiệm?
Trong thí nghiệm Y-âng, chiếu đồng thời hai bức xạ có bước sóng \({\lambda _1} = 0,45\mu m\)và \({\lambda _2} = 0,63\,\mu m.\) Trên màn quan sát, gọi M, N là hai điểm nằm cùng một phía so với vân trung tâm. Biết tại điểm M trùng với vị trí vân sáng bậc 5 của bức xạ \({\lambda _2}\), tại điểm N trùng với vị trí vân sáng bậc 14 của bức xạ \({\lambda _1}\). Tính số vân sáng quan sát được trên khoảng MN (không kể M, N) ?
Đáp án: ……….
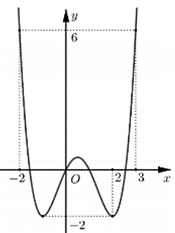
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{x^3} - 3x} \right) = m\) có 6 nghiệm thuộc đoạn \(\left[ { - 1\,;\,\,2} \right]?\)
Đồ thị nào dưới đây biểu diễn đúng sự biến đổi nồng độ các chất theo thời gian của phản ứng A + 2B → C?
Trên mặt phẳng tọa độ \[Oxy,\] cho hình bình hành \[ABCD\] có phương trình đường thẳng \[AB\] là \(2x + y + 7 = 0\), phương trình đường thẳng \[AD\] là \(x - 4y - 1 = 0\) và giao điểm của hai đường chéo \[AC,\,\,BD\] là \[I\left( {1\,;\,\,2} \right).\] Phương trình của đường thẳng \[BC\] là
Tập hợp các giá trị của \(m\) để hàm số \(y = - m{x^3} + {x^2} - 3x + m - 2\) nghịch biến trên khoảng \[\left( { - 3\,;\,\,0} \right)\] là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
Cho biểu đồ:
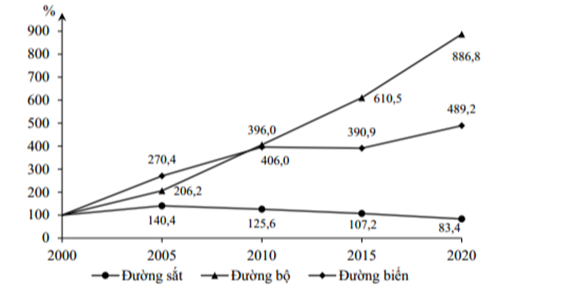
KHỐI LƯỢNG HÀNG HÓA VẬN CHUYỂN
MỘT SỐ NGÀNH VẬN TẢI NƯỚC TA GIAI ĐOẠN 2000-2020
(Nguồn: Niên giám Thống kê Việt Nam năm 2020, NXB Thống kê, 2021)
Biểu đồ thể hiện nội dung nào sau đây?
Cho hàm số bậc bốn \(y = f\left( x \right)\) có bảng biến thiên như sau:
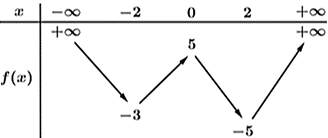
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = {e^{f\left( x \right)}} - m \cdot {3^{f\left( x \right)}}\) có đúng 7 điểm cực trị?