PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
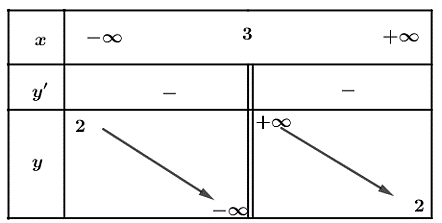
Cho hàm số ![]() xác định trên
xác định trên ![]() và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
a) Hàm số ![]() đồng biến trên mỗi khoảng
đồng biến trên mỗi khoảng ![]() và
và ![]() .
.
b) Số điểm cực trị của hàm số đã cho là ![]() .
.
c) Hàm số ![]() có giá trị nhỏ nhất bằng
có giá trị nhỏ nhất bằng ![]() .
.
d) Đồ thị hàm số không có đường tiệm cận.
 Giải bởi Vietjack
Giải bởi Vietjack
a) S, b) Đ, c) Đ, d) Đ.
Hướng dẫn giải
– Quan sát bảng biến thiên, ta thấy hàm số đã cho đồng biến trên mỗi khoảng ![]() và
và ![]() , do đó ý a) sai.
, do đó ý a) sai.
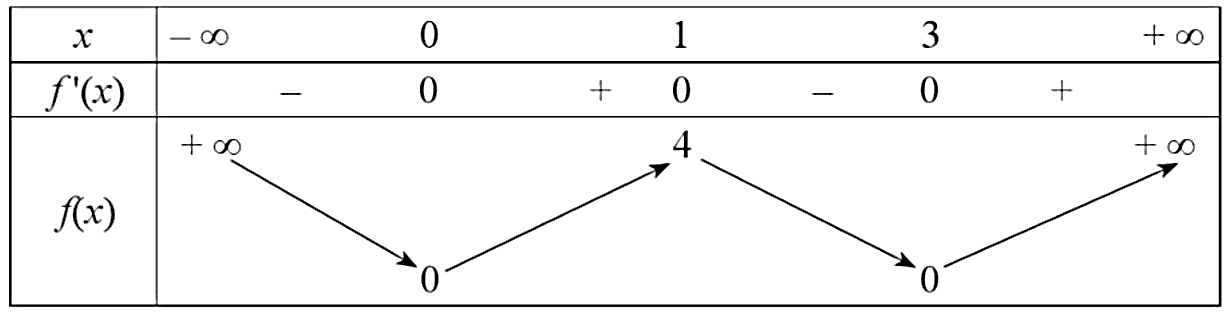
– Ta có ![]() đổi dấu từ “–” sang “+” tại các điểm
đổi dấu từ “–” sang “+” tại các điểm ![]() ,
, ![]() và đổi dấu từ “+” sang “–” tại điểm
và đổi dấu từ “+” sang “–” tại điểm ![]() . Vậy hàm số
. Vậy hàm số ![]() có 3 điểm cực trị nên ý b) đúng.
có 3 điểm cực trị nên ý b) đúng.
– Hàm số ![]() có giá trị nhỏ nhất bằng
có giá trị nhỏ nhất bằng ![]() tại
tại ![]() và
và ![]() nên ý c) đúng.
nên ý c) đúng.
– Hàm số ![]() xác định trên
xác định trên ![]() và
và ![]() nên đồ thị hàm số này không có đường tiệm cận. Vậy ý d) đúng.
nên đồ thị hàm số này không có đường tiệm cận. Vậy ý d) đúng.
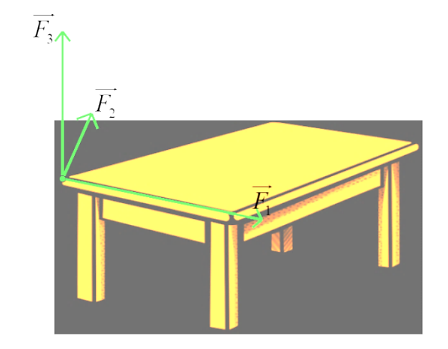
Có ba lực cùng tác động vào một cái bàn như hình vẽ dưới. Trong đó hai lực ![]() tạo với nhau một góc
tạo với nhau một góc ![]() và có độ lớn lần lượt là 9 N và 4 N, lực
và có độ lớn lần lượt là 9 N và 4 N, lực ![]() vuông góc với mặt phẳng tạo bởi hai lực
vuông góc với mặt phẳng tạo bởi hai lực ![]() và có độ lớn 7 N. Độ lớn hợp lực của ba lực trên là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị của Newton)?
và có độ lớn 7 N. Độ lớn hợp lực của ba lực trên là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị của Newton)?
Cho hàm số 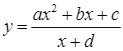 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Trong các số ![]() có bao nhiêu số có giá trị dương?
có bao nhiêu số có giá trị dương?
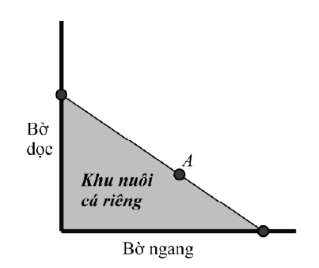
Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí ![]() . Diện tích nhỏ nhất có thể giăng lưới là bao nhiêu mét vuông, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
. Diện tích nhỏ nhất có thể giăng lưới là bao nhiêu mét vuông, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
Cho hàm số ![]() có đồ thị như hình dưới đây.
có đồ thị như hình dưới đây.
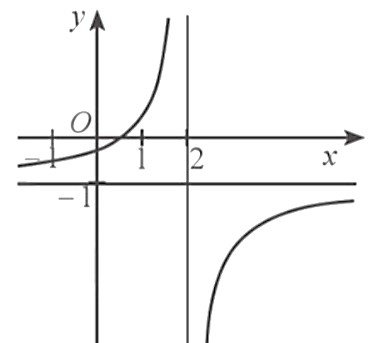
Phát biểu nào sau đây là đúng?
Cho hàm số ![]() có đồ thị như hình dưới đây.
có đồ thị như hình dưới đây.
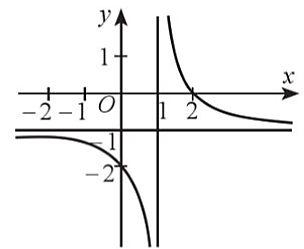
Tâm đối xứng của đồ thị hàm số có tọa độ là
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có đồ thị như hình dưới đây.
và có đồ thị như hình dưới đây.
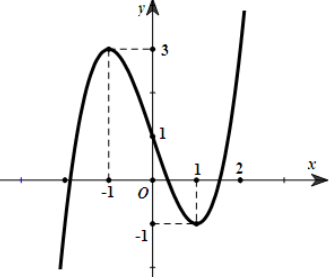
Phát biểu nào sau đây là đúng?
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
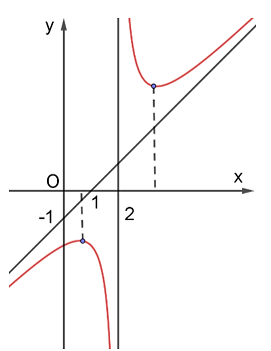
Cho hàm số ![]() có đồ thị như hình dưới đây.
có đồ thị như hình dưới đây.
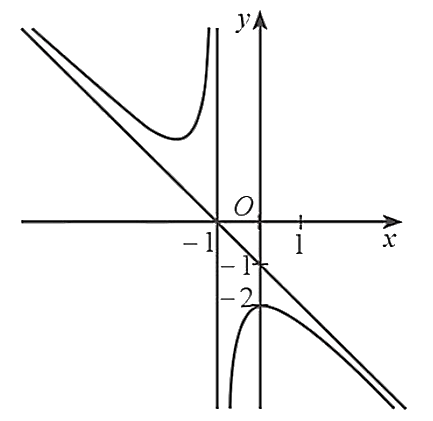
Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng
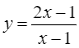 có đồ thị là
có đồ thị là Cho hàm số ![]() có đồ thị như hình dưới đây.
có đồ thị như hình dưới đây.
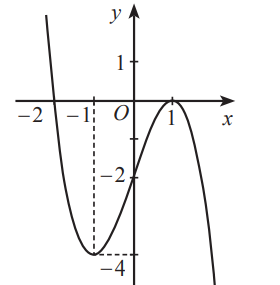
Giá trị nhỏ nhất của hàm số đã cho trên đoạn ![]() là:
là:
Quan sát bảng biến thiên và cho biết bảng biến thiên đó là của hàm số nào.