Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow a = \left( { - 2;1;2} \right)\), \(\overrightarrow b = \left( {1;1; - 1} \right)\).
a) Xác định tọa độ của \(\overrightarrow u = \overrightarrow a - 2\overrightarrow b \). (0,25 điểm)
b) Tính độ dài của \(\overrightarrow u \). (0,25 điểm)
c) Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). (0,5 điểm)
 Giải bởi Vietjack
Giải bởi Vietjack
a) Ta có: \(2\overrightarrow b = \left( {2;2; - 2} \right)\).
Do đó, \(\overrightarrow a - 2\overrightarrow b = \left( { - 2 - 2;1 - 2;2 - \left( { - 2} \right)} \right) = \left( { - 4; - 1;4} \right)\).
Vậy \(\overrightarrow u = \left( { - 4; - 1;4} \right)\).
b) Ta có: \(\left| {\overrightarrow u } \right| = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 1} \right)}^2} + {4^2}} = \sqrt {33} \).
Vậy độ dài vectơ \(\overrightarrow u \) là \(\sqrt {33} \).
c) Ta có: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 2.1 + 1.1 + 2.\left( { - 1} \right)}}{{\sqrt {{{\left( { - 2} \right)}^2} + {1^2} + {2^2}} .\sqrt {{1^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{ - \sqrt 3 }}{3}\).
Vậy \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{ - \sqrt 3 }}{3}\).
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f'\left( x \right)\) dưới đây:
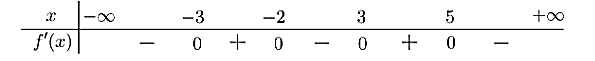
Số điểm cực trị của hàm số đã cho là:
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\).
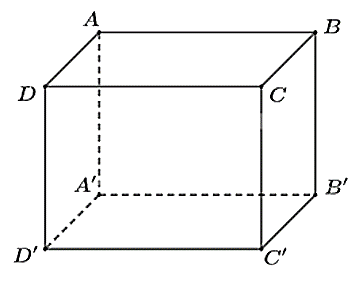
Mệnh đề nào sau đây là sai?
Cho hàm số \[y = f\left( x \right)\] có đồ thị hàm số như hình vẽ dưới đây.
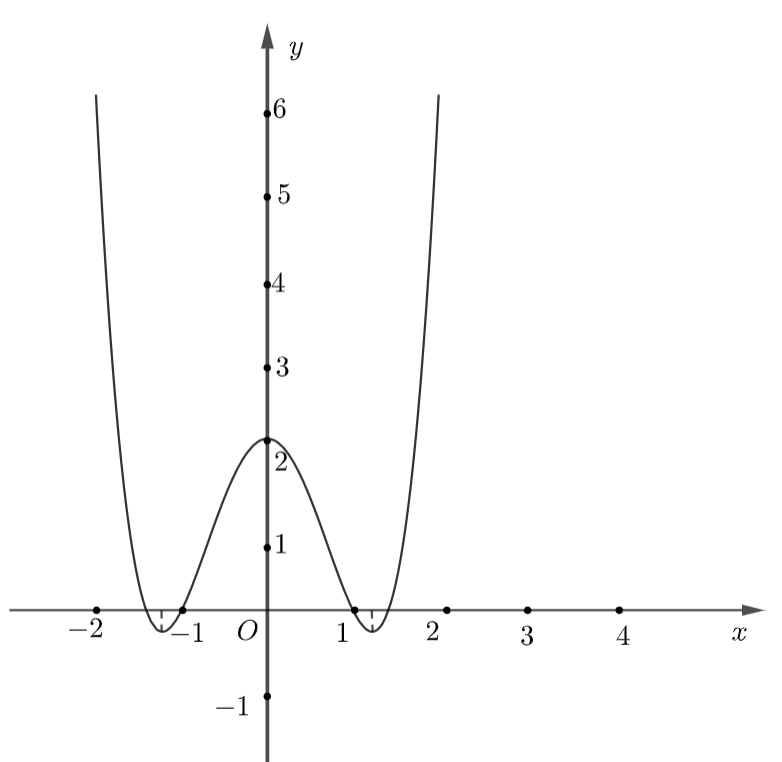
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Thể tích \(V\) (đơn vị: cm3) của 1 kg nước tại nhiệt độ \(T\left( {0^\circ C \le T \le 30^\circ C} \right)\) được tính bởi công thức sau: \(V(T) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}.\) (Nguồn: J. Stewart, Calculus, Steventh Edition, Brooks/Cole, CENGAGE Learning 2012).
Hỏi thể tích \(V\left( T \right)\),\(\left( {0^\circ C \le T \le 30^\circ C} \right)\), giảm trong khoảng nhiệt độ gần với khoảng nào sau đây?