Trong không gian \(Oxyz\), cho các điểm \(A\left( {1;3;5} \right)\), \(B\left( {1;1;3} \right)\), \(C\left( {4; - 2;3} \right)\).
Khi đó:
a) Tọa độ trung điểm \(BC\) là \(\left( {\frac{5}{2}; - \frac{1}{2};3} \right)\).
b) Độ dài đoạn thẳng \(BC\) là \(3\sqrt 2 \).
c) Côsin \(\widehat {BAC}\) bằng \(\frac{{7\sqrt {19} }}{{38}}\).
d) Gọi \(D\) là đỉnh thứ tư của hình bình hành \(ABCD\). Tọa độ hình chiếu của trọng tâm tam giác \(ABD\) lên mặt phẳng \(Oyz\) là \(\left( {2;0;0} \right)\).
Số mệnh đề đúng trong các mệnh đề trên là:
A. \(1.\)
B. \(2.\)
C. \(3.\)
D. \(4.\)
Giải bởi Vietjack
Đáp án đúng là: C
a) Gọi \(I\left( {x;y;z} \right)\) là trung điểm \(BC\).
Ta có: \(\left\{ \begin{array}{l}x = \frac{{1 + 4}}{2} = \frac{5}{2}\\y = \frac{{1 + \left( { - 2} \right)}}{2} = - \frac{1}{2}\\z = \frac{{3 + 3}}{2} = 3\end{array} \right.\) ⇒ \(I\left( {\frac{5}{2}; - \frac{1}{2};3} \right)\).
Vậy a đúng.
b) Ta có: \(\overrightarrow {BC} = \left( {3; - 3;0} \right)\) ⇒ \(BC = \sqrt {{3^2} + {{\left( { - 3} \right)}^2} + {0^2}} = 3\sqrt 2 \) suy ra b đúng.
c) Ta có: \(\overrightarrow {AB} = \left( {0; - 2; - 2} \right),\overrightarrow {AC} = \left( {3; - 5; - 2} \right)\).
Do đó, \(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}}\)
\( = \frac{{0.3 + \left( { - 2} \right).\left( { - 5} \right) + \left( { - 2} \right).\left( { - 2} \right)}}{{\sqrt {{0^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{3^2} + {{\left( { - 5} \right)}^2} + {{\left( { - 2} \right)}^2}} }} = \frac{{7\sqrt {19} }}{{38}}.\)
Vậy ý c đúng.
d) Gọi \(D\left( {x;y;z} \right)\). Có \(\overrightarrow {AB} = \overrightarrow {DC} \).
Ta có: \(\overrightarrow {AB} = \left( {0; - 2; - 2} \right)\), \(\overrightarrow {DC} = \left( {4 - x; - 2 - y;3 - z} \right)\).
Suy ra \(\left\{ \begin{array}{l}4 - x = 0\\ - 2 - y = - 2\\3 - z = - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 4\\y = 0\\z = 5\end{array} \right.\) ⇒ \(D\left( {4;0;5} \right)\).
Gọi \(G\left( {a;b;c} \right)\) là trọng tâm tam giác \(ABD\).
Ta có: \(\left\{ \begin{array}{l}a = \frac{{1 + 1 + 4}}{3} = 2\\b = \frac{{3 + 1 + 0}}{3} = \frac{4}{2}\\c = \frac{{5 + 3 + 5}}{3} = \frac{{13}}{3}\end{array} \right.\) ⇒ \(G\left( {2;\frac{4}{3};\frac{{13}}{3}} \right)\).
Tọa độ hình chiếu của trọng tâm \(G\) của tam giác \(ABD\) lên mặt phẳng \(Oyz\) là \(\left( {0;\frac{4}{3};\frac{{13}}{3}} \right)\).
Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất cách điểm xuất phát 2 km về phía nam và 1 km về phía đông, đồng thời cách mặt đất 0,5 km. chiếc thứ hai mằm cách điểm xuất phát 1 km về phía bắc và 1,5 km về phía tây, đồng thời cách mặt đất 0,8 m. Chọn hệ trục \(Oxyz\) với O là gốc đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất với trục \(Ox\) hướng về phía nam, trục \[Oy\] hướng về phía đông và trục \(Oz\) hướng thẳng đứng lên trời, đơn vị đo lấy theo kilomet.
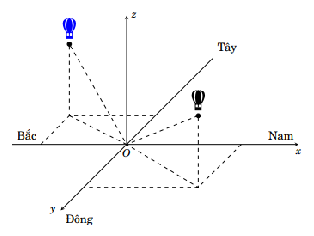
Khi đó:
a) Với hệ tọa độ đã chọn, tọa độ khinh khí cầu thứ nhất là \(\left( {2;1;0,5} \right)\).
b) Với hệ tọa độ đã chọn, tọa độ khinh khí cầu thứ hai là \(\left( { - 1,5; - 1;0,8} \right)\).
c) Khoảng cách từ điểm xuất phát đến khinh khí cầu thứ nhất bằng \(\sqrt {21} \) km.
d) Khoảng cách hai chiếc khinh khí cầu là 3,92 km (Kết quả làm tròn đến hàng phần trăm).
Số khẳng định đúng trong các khẳng định trên là:
Trong không gian \(Oxyz\), cho hình thang \(ABCD\) vuông tại \(A\) và \(B\). Ba đỉnh \(A\left( {1;2;1} \right)\), \(B\left( {2;0; - 1} \right)\), \(C\left( {6;1;0} \right)\). Hình thang có diện tích bằng \(6\sqrt 2 \). Giả sử đỉnh \(D\left( {a;b;c} \right)\), tìm mệnh đề đúng.
Trong không gian \(Oxyz\), cho điểm \(G\left( {1; - 2;3} \right)\) và ba điểm \(A\left( {a;0;0} \right)\), \(B\left( {0;b;0} \right)\), \(C\left( {0;0;c} \right)\). Biết \(G\) là trọng tâm của của tam giác \(ABC\) thì \(a + b + c\) bằng
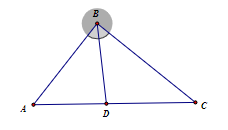
Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {1;2; - 1} \right)\), \(B\left( {2; - 1;3} \right)\), \(C\left( { - 4;7;5} \right)\). Gọi \(D\left( {a;b;c} \right)\) là chân đường phân giác trong góc \(B\) của tam giác \(ABC\). Giá trị \(a + b + 2c\) bằng
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( { - 1 - 1;0} \right)\) và \(\overrightarrow b = \left( {0; - 1;0} \right)\). Góc giữa hai vectơ này là:
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( {1; - 2;3} \right)\) và \(\overrightarrow b = \left( { - 2;1;2} \right)\). Tích vô hướng \(\left( {\overrightarrow a + \overrightarrow b } \right)\overrightarrow b \) bằng
Trong không gian \(Oxyz\), cho hai điểm \(M\left( {1; - 2;2} \right)\) và \(N\left( {1;0;4} \right)\). Tọa độ trung điểm của đoạn thẳng \(MN\) là
Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow u = \left( {1; - 2;3} \right)\). Vectơ nào sau đây cùng phương với vectơ \(\overrightarrow u \) ?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;2; - 5} \right)\), \(B\left( {1;2;4} \right)\), \(C\left( {2;5; - 2} \right)\). Tọa độ trọng tâm \(G\) của tam giác \(ABC\) là
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow u = \left( {1;2;3} \right)\) và \(\overrightarrow v = \left( {4; - 5;6} \right)\). Vectơ \(2\overrightarrow u - 3\overrightarrow v \) cùng phương với vectơ nào?
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {0;2;1} \right)\) và \(B\left( {3; - 2;1} \right)\). Độ dài đoạn thẳng \(AB\) bằng
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( {3;0;1} \right)\) và \(\overrightarrow c = \left( {1;1;0} \right)\). Tọa độ của vectơ \(\overrightarrow b \) thỏa mãn đẳng thức \(\overrightarrow b - \overrightarrow a + 2\overrightarrow c = \overrightarrow 0 \) là
Trong không gian \(Oxyz\), cho ba điểm \(M\left( {2; - 3; - 1} \right)\), \(N\left( {0;3;1} \right)\), \(P\left( {1;m - 1;2} \right)\). Với giá trị nào của \(m\) thì tam giác \(MNP\) vuông tại \(N\)?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( { - 1; - 2;3} \right)\), \(B\left( {0;3;1} \right)\), \(C\left( {4;2;2} \right)\). Giá trị \(\cos \left( {\widehat {BAC}} \right)\) bằng
Cho hai vectơ \(\overrightarrow u = \left( {2; - 2; - 3} \right)\) và \(\overrightarrow v = \left( {3;3;5} \right)\). Vectơ nào dưới đây vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) ?
