Biến ngẫu nhiên hai chiều rời rạc (X, Y) có bảng phân phối xác suất.E(X) =?
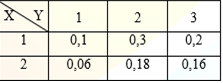
A. 2,2
B. 2,3
C. 2,4
D. 2,5
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án A
Công thức ước lượng khoảng tin cậy đối xứng (với độ tin cậy 1−α) cho kỳ vọng của biến ngẫu nhiên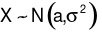 (σ chưa biết) là:
(σ chưa biết) là:
Có người nói tỷ lệ sản phẩm xấu của nhà máy tối đa là 7%. Kiểm tra 100 sản phẩm thấy 8 phế phẩm. Với mức ý nghĩa = 0,05, hãy kết luận ý kiến trên. Giá trị quan sát (Kiểm định thực nghiệm) nào là đúng dưới đây?
Có 12 học sinh giỏi gồm 3 học sinh khối 12, 4 học sinh khối 11 và 5 học sinh khối 10. Hỏi có bao nhiêu cách chọn ra 6 học sinh trong số học sinh giỏi đó sao cho mỗi khối có ít nhất 1 học sinh?
Đội văn nghệ của một nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Cần chọn ngẫu nhiên 5 học sinh từ đội văn nghệ đó để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn và có ít nhất 2 học sinh lớp 12A?
Công thức ước lượng giá trị tối thiểu (với độ tin cậy 1−α) cho kỳ vọng của biến ngẫu nhiên 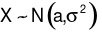 ( σ chưa biết) là:
( σ chưa biết) là:
Trong bài toán kiểm định giả thuyết cho kỳ vọng của biến ngẫu nhiên có phân phối chuẩn với cặp giả thuyết, đối thuyết 
Trường hợp σ2 đã biết, ta chọn thống kê để kiểm định là:
Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn?
Đội học sinh giỏi cấp trường môn Tiếng Anh của trường THPT X theo từng khối như sau: khối 10 có 5 học sinh, khối 11 có 5 học sinh và khối 12 có 5 học sinh. Nhà trường cần chọn một đội tuyển gồm 10 học sinh tham gia IOE cấp tỉnh. Tính số cách lập đội tuyển sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10
Một hộp đựng 8 viên bi màu xanh, 5 viên bi đỏ, 3 viên bi màu vàng. Có bao nhiêu cách chọn từ hộp đó ra 4 viên bi sao cho số bi xanh bằng số bi đỏ?
Công thức ước lượng khoảng tin cậy đối xứng (với độ tin cậy 1−α) cho kỳ vọng của biến ngẫu nhiên 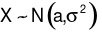 (σ đã biết) là:
(σ đã biết) là:
Một hộp có 10 phiếu, trong đó có 2 phiếu trúng thưởng. Có 10 người lần lượt lấy ngẫu nhiên mỗi người 1 phiếu. Tính xác suất người thứ ba lấy được phiếu trúng thưởng
Trong bài toán kiểm định giả thuyết cho kỳ vọng của biến ngẫu nhiên có phân phối chuẩn, với cặp giả thuyết, đối thuyết 
Trường hợp σ2 chưa biết, ta chọn thống kê để kiểm định là:
Trong bài toán kiểm định cho xác suất (tỷ lệ), với cặp giả thuyết, đối thuyết: 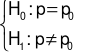 ta chọn thống kê để kiểm định là:
ta chọn thống kê để kiểm định là:
Biến ngẫu nhiên hai chiều rời rạc (X, Y) có bảng phân phối xác suất.E(Y) =?

Nếu biến ngẫu nhiên gốc tuân theo phân phối nhị thức 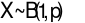 thì
thì 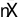 tuân theo phân phối?
tuân theo phân phối?