Cho hình nón chứa bốn mặt cầu cùng có bán kính là ![]() , trong đó ba mặt cầu tiếp xúc với đáy, tiếp xúc lẫn nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ tư tiếp xúc với ba mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón.
, trong đó ba mặt cầu tiếp xúc với đáy, tiếp xúc lẫn nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ tư tiếp xúc với ba mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón.

Tính bán kính đáy của hình nón.
 Giải bởi Vietjack
Giải bởi Vietjack
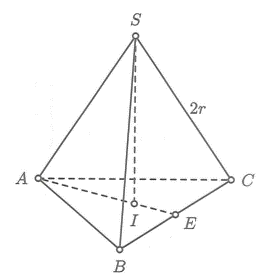
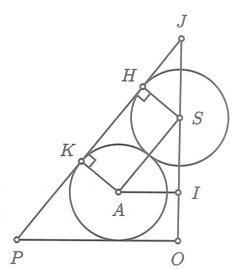
Xét trường hợp tổng quát là bốn mặt cầu có bán kính r.
Gọi tâm các mặt cầu là S, A, B, C, trong đó S là tâm của mặt cầu trên cùng.
Do các mặt cầu tiếp xúc ngoài nhau nên S.ABC là chóp đều cạnh 2r.
Gọi I là tâm của tam giác ABC, khi đó SI vuông góc với mặt phẳng ![]() và
và ![]() .
.
Tam giác SAI vuông tại I, có
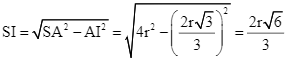 .
.
Kẻ đường sinh JP của hình nón tiếp xúc với hai mặt cầu tâm S và tâm A lần lượt tại H, K.
Ta có ![]() (g-g) nên
(g-g) nên ![]() .
.
![]() .
.
Chiều cao của khối nón là
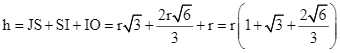 .
.
Bán kính khối nón là ![]() .
.
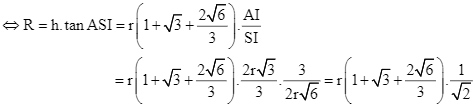
Áp dụng với ![]() ta được
ta được 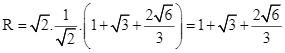 . Chọn C.
. Chọn C.
Điền đáp án chính xác vào chỗ trống.
Theo hình 1, 16 giờ sau khi dùng dạng viên nén giải phóng kéo dài của thuốc theo toa, sự chênh lệch về nồng độ trung bình giữa thành phần A và thành phần B trong huyết tương gần nhất với (1)_________ ng/ml.
Phát biểu sau đúng hay sai?
Sử dụng CuO bị lẫn tạp chất không làm ảnh hưởng đến kết quả của thí nghiệm 2.
Điền từ/cụm từ thích hợp vào chỗ trống.
Trong thí nghiệm 2, nếu CuO phản ứng với ![]() để tạo ra các sản phẩm không phải là
để tạo ra các sản phẩm không phải là ![]() thì _______ dùng thí nghiệm này để xác định tính đúng đắn của phản ứng:
thì _______ dùng thí nghiệm này để xác định tính đúng đắn của phản ứng:
![]()
Nhận định sau đây đúng hay sai?
Nồng độ trong huyết tương trung bình của thành phần B được sử dụng dưới dạng viên nang phóng thích tức thời luôn thấp hơn nồng độ trong huyết tương trung bình của thành phần A trong khoảng 24 giờ sau khi dùng thuốc.
Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng thứ mười hai bằng 23. Khi đó:
Số hạng đầu tiên của cấp số cộng đó là: _______.
Công sai của cấp số cộng là: _______.
Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây. Người ta đo được đường kính của miệng ly là ![]() và chiều cao là
và chiều cao là ![]() . Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng đối xứng là một parabol.
. Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng đối xứng là một parabol.

Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
![]()
![]()
![]()


Diện tích thiết diện là _______.
Tính thể tích của vật thể đã cho là V = _______.