I. Nhận biết
Góc ở tâm là góc
A. có hai cạnh là hai đường kính của đường tròn.
B. có đỉnh nằm trên đường tròn.
C. có đỉnh trùng với tâm đường tròn.
D. có đỉnh nằm trên bán kính của đường tròn.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.
Do đó ta chọn phương án C.
III. Vận dụng
Cho hình vẽ bên.

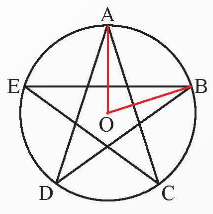
Số đo cung lớn \[AB\] trong hình ngôi sao năm cánh đã cho bằng
Cho nửa đường tròn đường kính \(AB\) và điểm \(C\) thuộc nửa đường tròn này sao cho \[\widehat {ABC} = 30^\circ \]. Số đo của cung \[BC\] là
Cho đường tròn \[\left( {O;R} \right)\] và dây cung \[MN = R\sqrt 3 .\] Kẻ \[OI \bot MN\] tại \[I.\] Số đo cung nhỏ \[MN\] bằng
Cho tam giác nhọn \[ABC\] có ba đỉnh nằm trên đường tròn \[\left( O \right)\]. Hai đường cao \[BD\] và \[CE\] cắt nhau tại \[H\]. Vẽ đường kính \[AF\] và gọi\[M\] là trung điểm \[BC\]. Cho các khẳng định sau:
(i) \(OM \bot BC\).
(ii) \(OM\,{\rm{//}}\,AH\).
(iii) \(HM = \frac{{HF}}{2}\).
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
II. Thông hiểu
Cho đường tròn \(\left( O \right)\) đi qua hai điểm \(A,\,\,B\). Biết \(\widehat {AOB} = 100^\circ \) thì số đo của cung lớn \(AB\) là
Cho đường tròn \(\left( O \right)\) đi qua ba điểm \(A,\,\,B,\,\,C\). Biết \(\widehat {ACB} = 56^\circ ,\) số đo của cung nhỏ \(AB\) là
Cho tam giác nhọn \[ABC\] có 3 đỉnh nằm trên đường tròn \[\left( O \right)\], đường kính \[BD\] . Biết \(\widehat {BAC} = 45^\circ \). Số đo của góc \[\widehat {CBD}\] là
Cho \[ABC\] nhọn có ba đỉnh nằm trên đường tròn \[\left( O \right)\] đường kính \(BD\). Vẽ tia \[Bx\] sao cho tia \(BC\) nằm giữa hai tia \(Bx,\,\,BD\) và \(\widehat {xBC} = \widehat {A\,}\). Số đo góc \(\widehat {OBx}\) là
Cho tam giác \[ABC\] có ba đỉnh nằm trên đường tròn \[\left( {O;{\rm{ }}R} \right)\], đường cao \[AH\], biết \[AB = 12{\rm{ cm}}\], \[AC = 15\,\,{\rm{cm}}\], \[AH = 6\,\,{\rm{cm}}\]. Đường kính của đường tròn \[\left( O \right)\] bằng
Cho đường tròn \[\left( {O;R} \right)\] và điểm \[A\] nằm trên đường tròn \[\left( {O;R} \right).\] Gọi \[H\] là điểm thuộc bán kính \[OA\] sao cho \[OH = \frac{{\sqrt 3 }}{2}OA.\] Dây \[CD\] vuông góc với \[OA\] tại \[H.\] Số đo cung lớn \[CD\] bằng