Giả sử chi phí tiền xăng ![]() (đồng) phụ thuộc tốc độ trung bình
(đồng) phụ thuộc tốc độ trung bình ![]() theo công thức:
theo công thức: 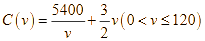 . Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?
. Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?
 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời: 60
Ta có ![]() ;
;
![]()
![]() (loại) hoặc
(loại) hoặc ![]() (nhận).
(nhận).
Trên khoảng ![]() ,
, ![]() nên hàm số nghịch biến trên khoảng này.
nên hàm số nghịch biến trên khoảng này.
Trên khoảng ![]() ,
, ![]() nên hàm số đồng biến trên khoảng này.
nên hàm số đồng biến trên khoảng này.
Hàm số đạt cực tiểu tại ![]() .
.
Như vậy để tiết kiệm xăng nhất tài xế nên chạy xe với tốc độ trung bình là 60 km/h.
Cho hàm số ![]() , (tham số
, (tham số ![]() ). Xét tính đúng sai của các khẳng định sau
). Xét tính đúng sai của các khẳng định sau
a) Khi ![]() thì hàm số đạt cực tiểu tại
thì hàm số đạt cực tiểu tại ![]() .
.
b) Khi ![]() thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng ![]() .
.
c) Khi ![]() thì hàm số có giá trị nhỏ nhất trên khoảng
thì hàm số có giá trị nhỏ nhất trên khoảng ![]() bằng
bằng ![]() .
.
d) Có tất cả 1 giá trị nguyên của ![]() để hàm số có giá trị nhỏ nhất trên khoảng
để hàm số có giá trị nhỏ nhất trên khoảng ![]() .
.
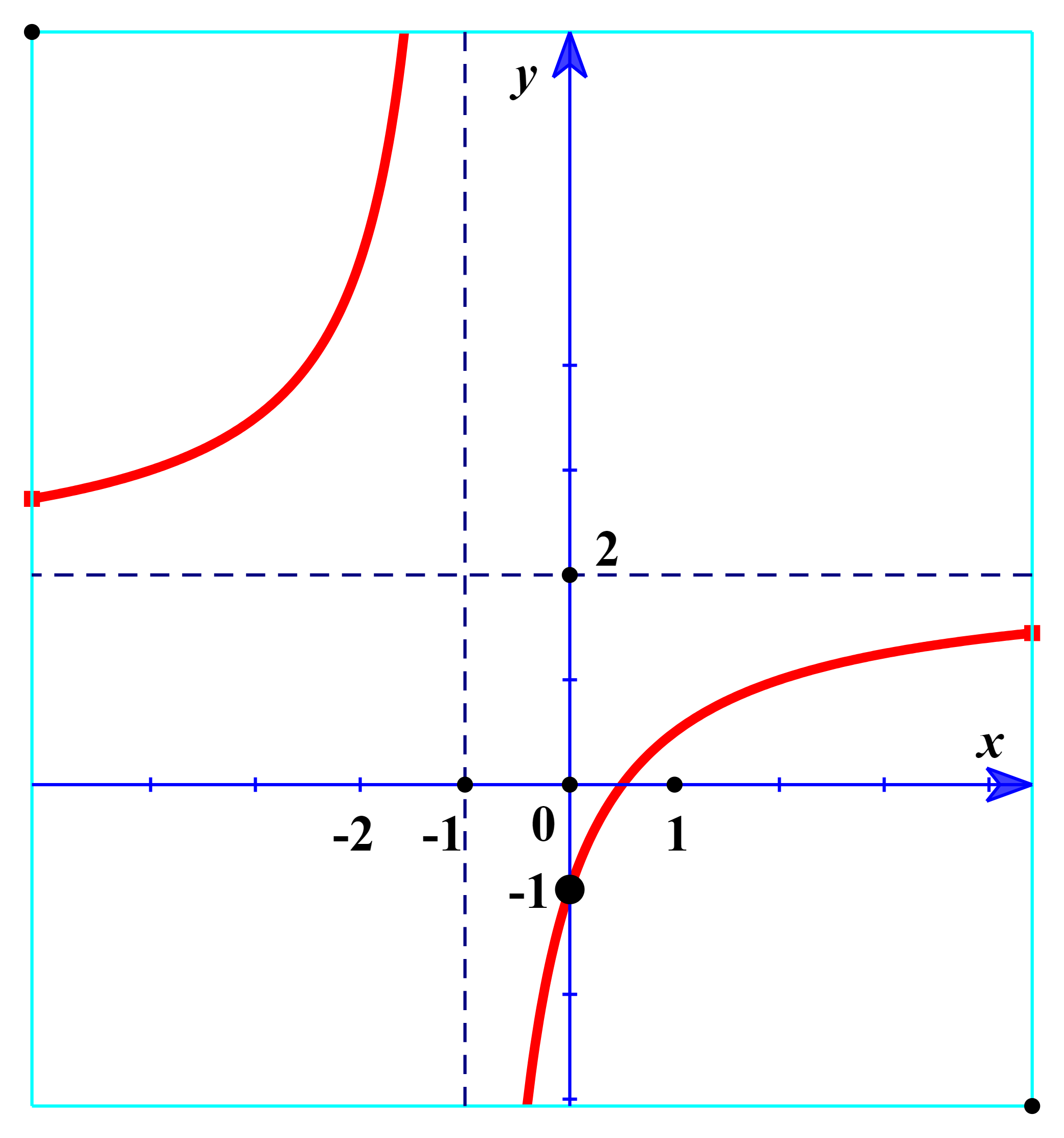
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả khảo sát được ghi lại ở bảng sau:
|
Mức giá (triệu đồng/ |
[10;14) |
[14;18) |
[18;22) |
[22;26) |
[26;30) |
|
Số khách hàng |
54 |
78 |
120 |
45 |
12 |
Khoảng biến thiên ![]() của mẫu số liệu ghép nhóm trên là.
của mẫu số liệu ghép nhóm trên là.
Bác tài xế A và bác tài xế B thống kê lại độ dài quãng đường (đơn vị: km) mà hai bác đã lái xe mỗi ngày trong một tháng ở bảng sau:
|
Độ dài quãng đường (km) |
|
|
|
|
|
|
Số ngày bác tài A lái xe |
5 |
10 |
9 |
4 |
2 |
|
Số ngày bác tài B lái xe |
4 |
8 |
12 |
6 |
0 |
a) Khoảng biến thiên về độ dài quãng đường đi mỗi ngày của bác tài A và B ở mẫu số liệu trên bằng nhau.
b) Tứ phân vị thứ nhất của mẫu số liệu về độ dài quãng đường mỗi ngày của bác tài A lớn hơn bác tài B
c) Tứ phân vị thứ ba của mẫu số liệu về quãng đường mỗi ngày của bác tài B thuộc nhóm ![]() .
.
d) Theo khoảng biến thiên thì độ dài quãng đường mỗi ngày của bác tài A phân tán hơn độ dài quãng đường mỗi ngày bác tài B.
Thời gian chạy tập luyện cự li ![]() của một vận động viên được cho trong bảng sau:
của một vận động viên được cho trong bảng sau:
|
Thời gian ( giây) |
|
|
|
|
|
|
Số lần chạy |
3 |
8 |
6 |
2 |
1 |
Tính phương sai của mẫu số liệu ghép nhóm trên.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() có bảng biến thiên như hình vẽ
có bảng biến thiên như hình vẽ
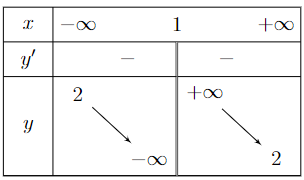 a) Hàm số đã cho nghịch biến trên
a) Hàm số đã cho nghịch biến trên ![]() .
.
b) Giá trị nhỏ nhất của hàm số là 2.
c) Tâm đối xứng của đồ thị hàm số là ![]() .
.
d) Có 2024 số nguyên ![]() trên
trên ![]() để phương trình
để phương trình ![]() có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số ![]() có bảng xét dấu của đạo hàm như sau
có bảng xét dấu của đạo hàm như sau
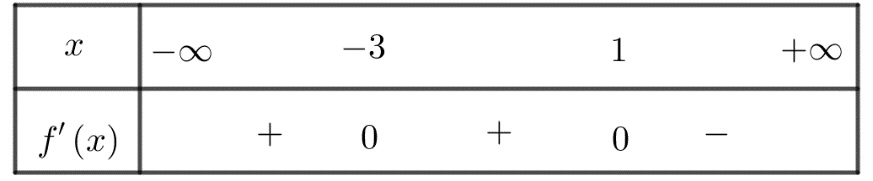
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?