PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Gọi ![]() lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số ![]() trên đoạn
trên đoạn ![]() . Tổng
. Tổng ![]() bằng bao nhiêu?
bằng bao nhiêu?
 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời: 0
Ta có ![]()
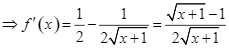 .
.
Ta có ![]() .
.
Ta có ![]() và hàm số
và hàm số ![]() liên tục trên đoạn
liên tục trên đoạn ![]() .
.
Vậy ![]()
![]() .
.
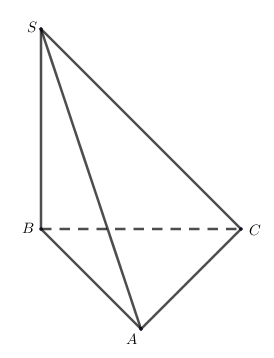
Cho tứ diện ![]() có đáy là tam giác đều cạnh
có đáy là tam giác đều cạnh ![]() ,
, ![]() vuông góc với đáy và
vuông góc với đáy và ![]() . Góc giữa hai vectơ
. Góc giữa hai vectơ ![]() là
là
Thống kê chỉ số chất lượng không khí (AQI) tại một địa điểm vào các ngày trong tháng 6/2022 được cho trong bảng sau
|
Chỉ số AQI |
|
|
|
|
|
|
Số ngày |
5 |
11 |
7 |
4 |
3 |
Khoảng biến thiên ![]() của mẫu số liệu ghép nhóm trên là.
của mẫu số liệu ghép nhóm trên là.
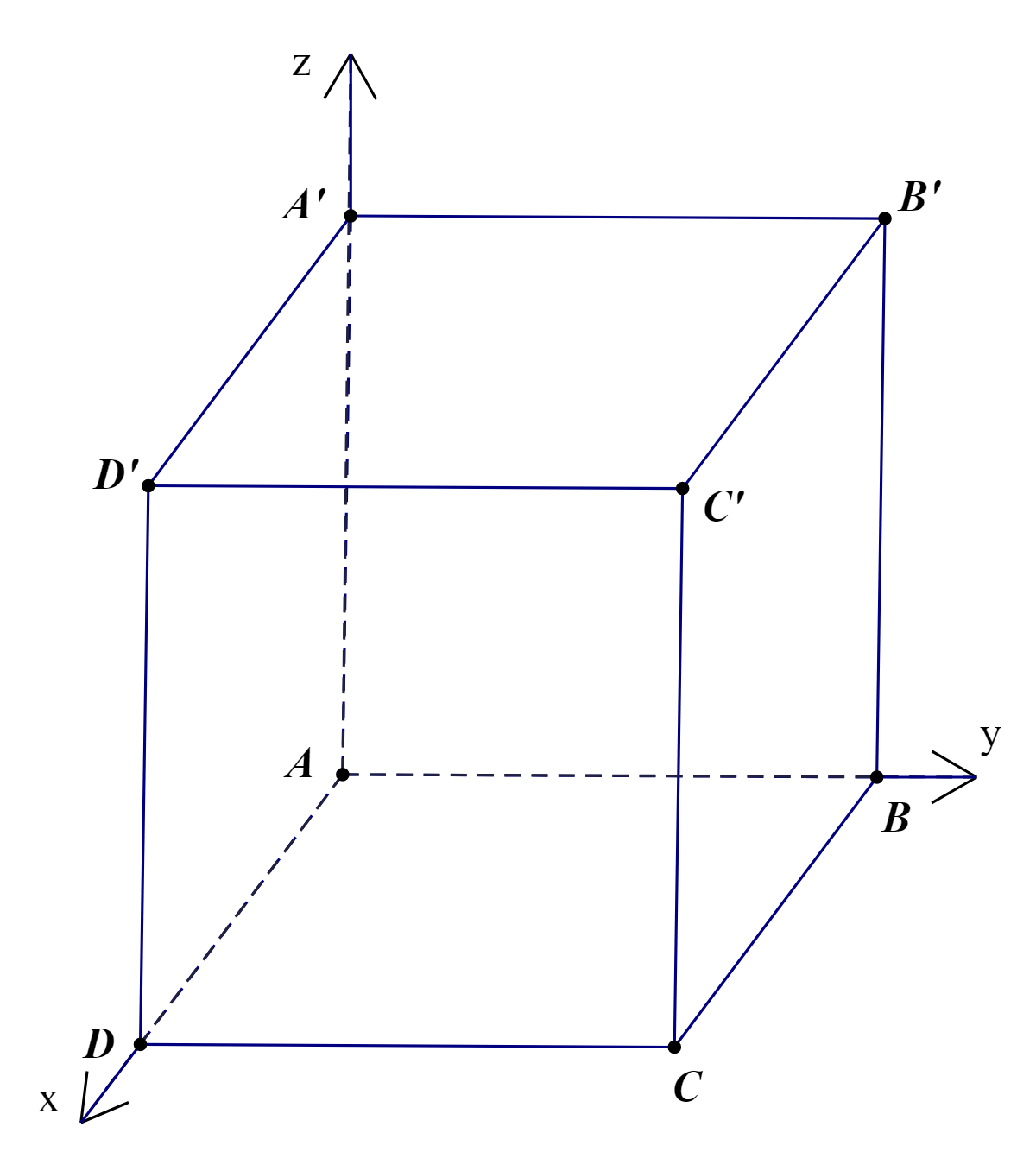
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 10 m, chiều rộng là 6m và
chiều cao là 4 m. Một chiếc quạt được treo trên trần nhà sao cho là điểm chính giữa của phòng học.
Xét hệ trục tọa độ ![]() có gốc (
có gốc (![]() ) trùng với một góc phòng và mặt phẳng (
) trùng với một góc phòng và mặt phẳng (![]() ) trùng với mặt sàn, đơn vị đo được lấy theo mét . Gọi
) trùng với mặt sàn, đơn vị đo được lấy theo mét . Gọi ![]() là tọa độ của điểm treo quạt. Tính giá trị
là tọa độ của điểm treo quạt. Tính giá trị ![]() ?
?
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
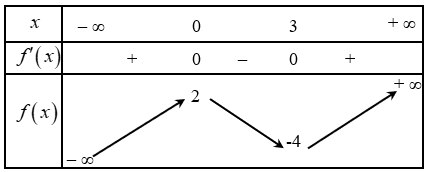
Đồ thị hàm số ![]() có điểm cực tiểu là
có điểm cực tiểu là
Cho hàm số ![]() liên tục trên đoạn
liên tục trên đoạn ![]() và có đồ thị như hình vẽ sau
và có đồ thị như hình vẽ sau
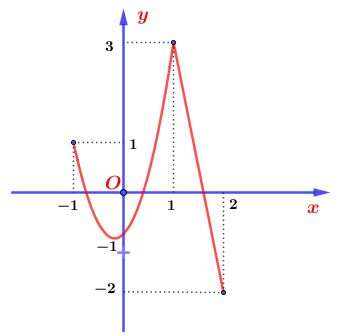
Giá trị lớn nhất của hàm số ![]() trên đoạn
trên đoạn ![]() là
là
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() xác định và liên tục trên
xác định và liên tục trên ![]() có bảng biến thiên như hình vẽ dưới đây. Xét tính đúng sai của các khẳng định sau:
có bảng biến thiên như hình vẽ dưới đây. Xét tính đúng sai của các khẳng định sau:
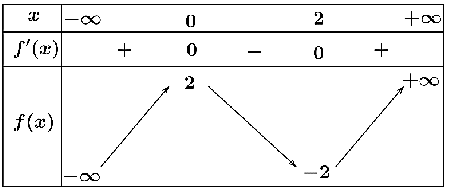
a) Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() và
và ![]() .
.
b) Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() .
.
c) ![]() .
.
d) Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() .
.
Cho hàm số ![]() (với tham số
(với tham số ![]() ). Xét tính đúng sai của các khẳng định sau:
). Xét tính đúng sai của các khẳng định sau:
a) Khi ![]() hàm số đồng biến trên mỗi khoảng
hàm số đồng biến trên mỗi khoảng ![]() và
và ![]() .
.
b) Khi ![]() thì trên đoạn
thì trên đoạn ![]() hàm số đạt giá trị lớn nhất bằng
hàm số đạt giá trị lớn nhất bằng ![]() .
.
c) ![]() là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
d) Có 1 giá trị của tham số ![]() để giá trị lớn nhất của hàm số
để giá trị lớn nhất của hàm số ![]() trên đoạn
trên đoạn ![]() bằng
bằng ![]() .
.
Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() .
.
a) Hình chiếu của điểm ![]() trên trục
trên trục ![]() có tọa độ là
có tọa độ là ![]() .
.
b) Gọi ![]() là điểm đối xứng của điểm
là điểm đối xứng của điểm ![]() qua
qua ![]() . Tọa độ của điểm
. Tọa độ của điểm ![]() là
là ![]() .
.
c) Cho ![]() . Tam giác
. Tam giác ![]() vuông tại N khi và chỉ khi
vuông tại N khi và chỉ khi ![]() .
.
d) Điểm ![]() nằm trên mặt phẳng
nằm trên mặt phẳng ![]() thỏa mãn
thỏa mãn ![]() đạt giá trị nhỏ nhất. Khi đó
đạt giá trị nhỏ nhất. Khi đó ![]() .
.