Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 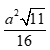
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
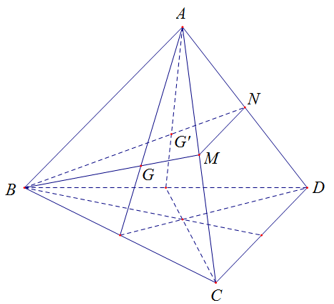
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
(BGG’)(ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = CD = ( MN là đường trung bình của tam giác ACD)
BM = BN = (BM, BN lần lượt là đường trung tuyến - đường cao của tam giác đều ABC, ABD có độ dài cạnh bằng a)
Áp dụng công thức hê- rông :
Trong đó: là nửa chu vi của tam giác
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Gọi P là giao điểm của SC và (AND). AN cắt DP tại I. SABI là hình gì?
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (AMN) và mp (BCD) là:
Cho mặt phẳng (P) và đường thẳng d(P). Mệnh đề nào sau đây đúng:
Cho hai mặt phẳng (P) và (Q) song song với nhau. Mệnh đề nào sau đây sai:
Cho hai đường thẳng phân biệt a và b cùng song song với mp (P). Có bao nhiêu vị trí tương đối của a và b?
Xét các mệnh đề:
(I) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua ba điểm.
(II) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua một điểm và chứa 1 đường thẳng.
(III) Mặt phẳng hoàn toàn được xác định khi biết nó chứa hai đường thẳng cắt nhau.
Số khẳng định đúng là
Cho 2 mặt phẳng (P) và (Q) cắt nhau theo giao tuyến . Hai đường thẳng p và q lần lượt nằm trong (P) và (Q). Trong các mệnh đề sau, mệnh đề nào đúng?
Trong các điều kiện sau, điều kiện nào kết luận đường thẳng a song song với mp (P)
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (MBC) và mp (NDA) là:
Cho hai hình bình hành ABCD và ABEF nằm trong 2 mặt phẳng phân biệt. Kết quả nào sau đây là đúng?
Chọn câu trả lời đúng:Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó?