Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
b) Gọi O là trung điểm của BD. Chứng minh AC, BD, MN đồng quy tai O.
 Giải bởi Vietjack
Giải bởi Vietjack
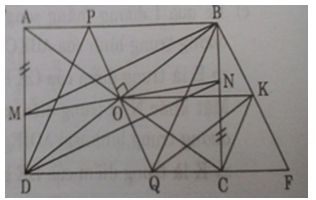
b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
b) Chứng I là trung điểm của DF.
Cho tứ giác ABCD có các tia phân giác của các góc ∠C và ∠D cắt nhau tại I. Số đo góc ∠CID là:
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
a) Chứng minh tứ giác EFDH là hình thang cân.
Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
d) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. Chứng minh rằng: AC ⊥ CK.
Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
a) Chứng minh rằng: BM // DN.
Chọn kết quả đúng: Cho hình thang ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AD và BC. Biết AB = 3cm và MN = 7cm. Độ dài cạnh CD là:
Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
c) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt cạnh CD tại Q. chứng minh rằng PBQD là hình thoi.
Cho ΔMNP vuông tại M, đường cao MH. Gọi K, I lần lượt là chân đường cao kẻ từ H đến MN và MP. Gọi L là trung điểm của HP. Số đo góc ∠KIL là:
Chọn đúng (Đ), sai (S) điền vào chỗ chấm: b) Hình chữ nhật là tứ giác có tất cả các góc bằng nhau. ....
Chọn đúng (Đ), sai (S) điền vào chỗ chấm: a) Tứ giác có hai đường chéo bằng nhau là hình chữ nhật. ....