Cho tam giác ABC cân tại A có Dựng qua A tia Ax vuông góc với AC và tia Ay vuông góc với AB, các tia Ax, Ay lần lượt cắt cạnh BC tại D và E (D,E ∈ BC). Chứng minh BD2 = BC.DE.
Giải bởi Vietjack
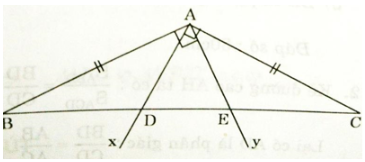
Ta có: Ax ⊥ AC (gt)
⇒ ∠DAC = 90o
⇒ ∠BAD = 135o - 90o = 45o
Tương tự ta có :
∠CAE = ∠BAD = 45o
Do đó AE và AB là phân giác trong và ngoài của góc ∠DAC
Ta có :
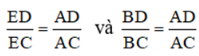
Xét ΔBAD và ΔCAE có:
∠BAD = ∠CAE ( = 45o )
AB = AC ( Δ ABC cân tại A)
∠ABD = ∠ACE (Δ ABC cân tại A)
⇒ ΔBAD = ΔCAE (g.c.g)
⇒ BD = EC
Thay vào (1) ta có : BD2 = BC.DE (đpcm).
