Cho hình hộp chữ nhật MNPQ.EFGH
a) Tìm giao tuyến của hai mặt phẳng (MNFE) và (QNFH).
b) Chứng minh: QH ⊥ mp(EFGH)
Giải bởi Vietjack
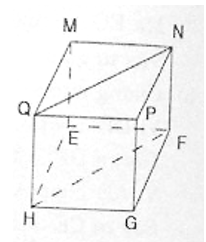
a) Ta có:
NF ⊂ mp(MNEF)
NF ⊂ mp(QNFH)
=> NF là giao uyến của hai mặt phẳng (MNFE) và (QNFH)
b) Ta có: QH ⊥ HE (do QHEM là hình chữ nhật)
QH ⊥ HG (do QHGP là hình chữ nhật)
Mà HE ∩ HG = {H}. Suy ra QH ⊥ mp(EFGH)
Cho một hình lăng trụ đứng có đáy là ngũ giác thì lăng trụ đó có:
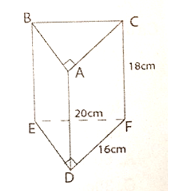
Cho một hình lăng trụ đứng ABC.DEF, đáy là tam giác vuông có kích thước như hình bên. Thể tích hình lăng trụ này là:
Cho hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao của hình chóp là 4cm. Tính:
a) Diện tích xung quanh của hình chóp
b) Thể tích của hình chóp.
Cho hình hộp chữ nhật ABCD.A'B'C'D', ta có:
