Tìm tất cả các giá trị thực của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
A.
B.
C. m = -1
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
![]()
![]()
![]() là tam thức bậc hai có ∆' = m2.
là tam thức bậc hai có ∆' = m2.
Do đó: y có cực đại cực tiểu ⇔ y’ có hai nghiệm phân biệt
⇔ g(x) có hai nghiệm phân biệt ⇔ ∆' > 0 ⇔ m ≠ 0. (1)
Khi đó, y’ có các nghiệm là: 1 ± m
→ tọa độ các điểm cực trị của đồ thị hàm số là
![]()
![]()
![]()
![]()
![]()
Để A và B cách đều gốc tọa độ khi và chỉ khi :
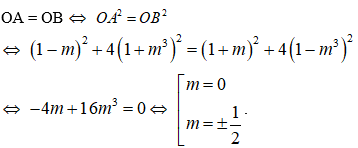
Đối chiếu với điều kiện (1), ta thấy chỉ thỏa mãn yêu cầu bài toán.
Cho hàm số có đồ thị (C) và đường thẳng Tất cả các giá trị của tham số m để d cắt (C) tại bốn điểm phân biệt là
Hàm số có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
Cho hàm số y = f(x) có đồ thị như hình vẽ:
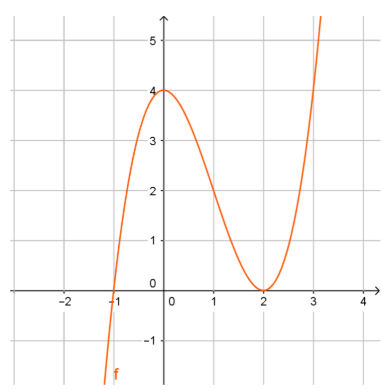
Đồ thị hàm số y = f(x) có mấy điểm cực trị?
Cho hàm số có đồ thị (C) và Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A; B sao cho tiếp tuyến tại A và B song song với nhau.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
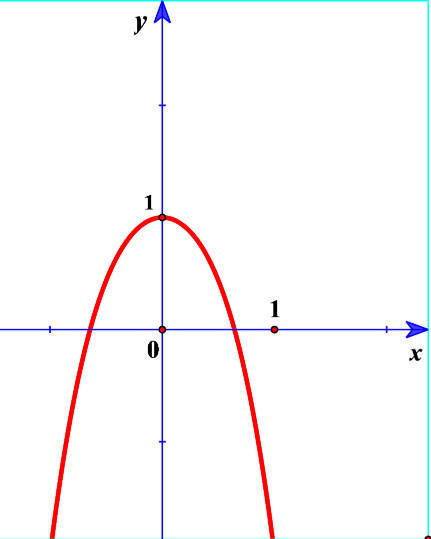
Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng (0;+∞)?