Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 1)
-
5832 lượt thi
-
25 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số . Khẳng định nào sau đây là khẳng đinh đúng?
 Xem đáp án
Xem đáp án
Chọn D.
![]()
![]()
Hàm số đồng biến trên các khoảng
Câu 2:
Cho hàm số y = f(x) có đồ thị như hình vẽ:
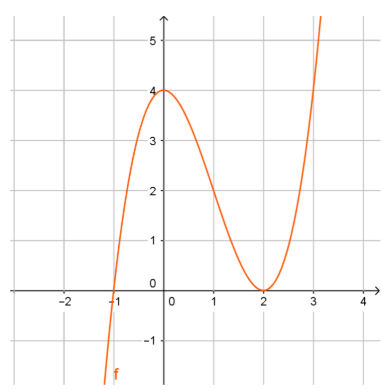
Đồ thị hàm số y = f(x) có mấy điểm cực trị?
 Xem đáp án
Xem đáp án
Chọn A
Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực đại tại x = 0, hàm số đạt cực tiểu tại x = 2.
Vậy đồ thị hàm số có 2 điểm cực trị.
Chọn D
Câu 3:
Hàm số nào sau đây có cực trị?
 Xem đáp án
Xem đáp án
![]()
Do đó, hàm số luôn đồng biến trên R. Hàm số này không có cực trị.
+ B. Hàm số trùng phương luôn luôn có cực trị.
![]()
+ Đối với phương án C và D, đây là hàm số bậc nhất và phân thức hữu tỉ bậc nhất /bậc nhất. Đây là 2 hàm số luôn đơn điệu trên từng khoảng xác định của chúng, do đó 2 hàm số này không có cực trị.
Chọn B
Câu 4:
Giá trị lớn nhất của hàm số trên đoạn [1; 3] là:
 Xem đáp án
Xem đáp án
Chọn B.
Nhận xét: Hàm số f(x) liên tục trên [1;3]
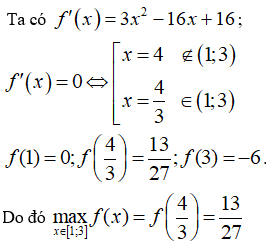
Câu 5:
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
 Xem đáp án
Xem đáp án
Chọn C
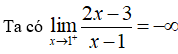
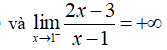
nên đồ thị hàm số có tiệm cận đứng là x = 1.
+) Lại có: ![]() nên đồ thị hàm số có tiệm cận ngang là y = 2.
nên đồ thị hàm số có tiệm cận ngang là y = 2.
Chọn C
Câu 6:
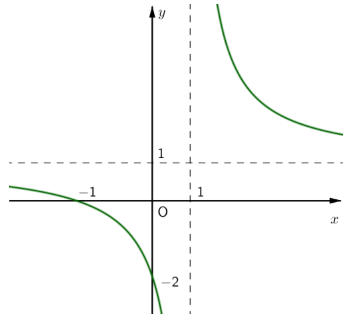
Đồ thị như hình vẽ là của hàm số nào sau đây :
 Xem đáp án
Xem đáp án
Chọn C
Từ đồ thị ta thấy có tiệm cận đứng là x = 1 và y = 1 → loại A,B
Giao điểm của đồ thị hàm số với trục tung là (0; -2) → chọn C.
Câu 7:
Cho hàm số có đồ thị (C). Kết luận nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Chọn C
Xét phương trình: mx + 9 = 0 (1)
Với x = -m; (1) trở thành : - m2 + 9 = 0 ⇔ m = ±3
Kiểm tra thấy với m = ±3 thì hàm số không có tiệm cận đứng và tiệm cận ngang.
Khi m ≠ ±3 hàm số luôn có tiệm cận đứng x = m hoặc x = -m và tiệm cận ngang y = m.
Chọn D
Câu 8:
Hàm số có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
 Xem đáp án
Xem đáp án
Chọn A.
Hàm số có tiệm cận đứng x = 1.
Tiệm cận ngang y = 1 nên loại trường hợp D.
Đồ thị hàm số đi qua điểm (0; 2) nên chọn đáp án A.
Câu 9:
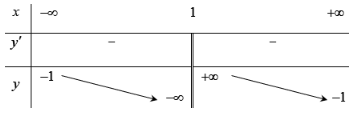
Cho hàm số y = f(x) có bảng biến thiên sau. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn A.
Nhìn vào bảng biến thiên ta thấy đồ thị có tiệm cận đứng x = 1; tiệm cận ngang y = -1
Câu 10:
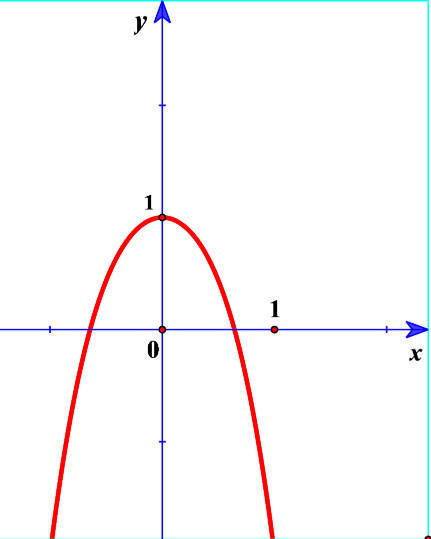
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
 Xem đáp án
Xem đáp án
Chọn D.
Từ đồ thị và đáp án suy ra đây là hàm số bậc 4 trùng phương: ![]() có 1 cực trị và hướng xuống nên a < 0; b < 0 nên loại A, B, C.
có 1 cực trị và hướng xuống nên a < 0; b < 0 nên loại A, B, C.
Câu 11:
Đồ thị hàm số có hai đường tiệm cận ngang với
 Xem đáp án
Xem đáp án
Chọn A
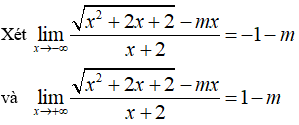
Để hàm số có hai tiệm cận ngang thì -1-m ≠ 1-m (thỏa với mọi m) .
Vậy ∀ m ∈ R thì đồ thị hàm số có hai tiệm cận ngang.
Câu 12:
Tìm tất cả các giá trị của tham số m để hàm số đạt cực đại tại x = 1.
 Xem đáp án
Xem đáp án
Chọn B
+ Để hàm số đạt cực đại x = 1 thì
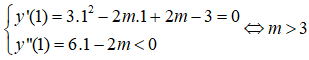
Câu 13:
Đồ thị cắt đường thẳng tại các điểm có tọa độ là
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm:
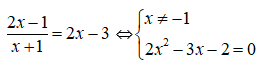
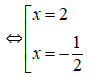
Thế vào phương trình y = 2x - 3 được tung độ tương ứng: 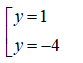
Vậy đồ thị (C) cắt đường thẳng d tại 2 điểm là
Câu 15:
Cho hàm số có đồ thị (C) và đường thẳng Tất cả các giá trị của tham số m để d cắt (C) tại bốn điểm phân biệt là
 Xem đáp án
Xem đáp án
Chọn C.
Xét hàm số y = x4- 4x2 - 2
Tính y’ = 4x3 – 8x
![]()
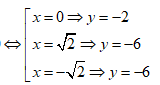
Bảng biến thiên:
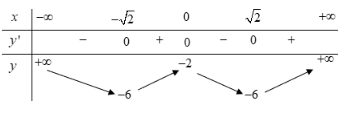
Dựa vào bảng biến thiên suy ra để đồ thị hàm số (C) cắt d tại 4 điểm phân biệt khi và chỉ khi: - 6 < m < -2.
Câu 16:
Cho hàm số có đồ thị (C) và Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A; B sao cho tiếp tuyến tại A và B song song với nhau.
 Xem đáp án
Xem đáp án
Chọn A.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d
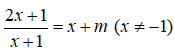
![]()
Khi đó d cắt (C) tại hai điểm phân biệt A; B khi và chi khi phương trình (1) có hai nghiệm phân biệt khác -1.
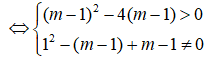
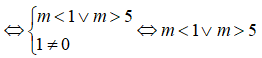
![]()
![]() trong đó x1, x2 là nghiệm của (1) (nên ta có
trong đó x1, x2 là nghiệm của (1) (nên ta có 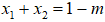
Suy ra hệ số góc của các tiếp tuyến tại điểm A và B lần lượt là
![]()
Vì tiếp tuyến tại A và B song song, đồng thời x1 ≠ x2 nên phải có
![]()
suy ra
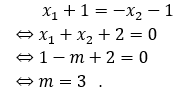
Kết hợp điều kiện ,vậy không có giá trị nào của m thỏa mãn.
Câu 17:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số giảm trên các khoảng mà nó xác định ?
 Xem đáp án
Xem đáp án
Chọn D
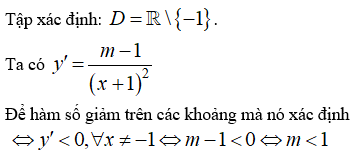
Câu 18:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng (0;+∞)?
 Xem đáp án
Xem đáp án
Chọn D.
Cách 1: Tập xác định: D = R. Ta có ![]()
+) Trường hợp 1:
![]()
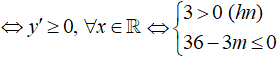
![]()
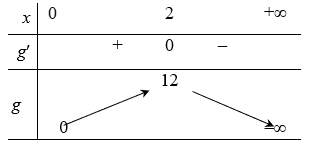
+) Trường hợp 2: Hàm số đồng biến trên (0; +∞) ⇔ y' = 0 có hai nghiệm x1; x2 thỏa mãn x1 < x2 ≤ 0(*)
-) Trường hợp 2.1: y’ = 0 có nghiệm x = 0 suy ra m = 0.
Nghiệm còn lại của y’ = 0 là x = 4 (không thỏa (*))
-) Trường hợp 2.2: y’ = 0 có hai nghiệm x1; x2 thỏa mãn:
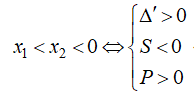
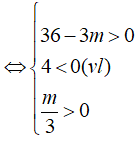
![]()
Kết hợp 2 trường hợp, vậy m ≥ 12
![]()
![]()
![]()
Câu 19:
Tìm tất cả các giá trị thực của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
 Xem đáp án
Xem đáp án
Chọn A
![]()
![]()
![]() là tam thức bậc hai có ∆' = m2.
là tam thức bậc hai có ∆' = m2.
Do đó: y có cực đại cực tiểu ⇔ y’ có hai nghiệm phân biệt
⇔ g(x) có hai nghiệm phân biệt ⇔ ∆' > 0 ⇔ m ≠ 0. (1)
Khi đó, y’ có các nghiệm là: 1 ± m
→ tọa độ các điểm cực trị của đồ thị hàm số là
![]()
![]()
![]()
![]()
![]()
Để A và B cách đều gốc tọa độ khi và chỉ khi :
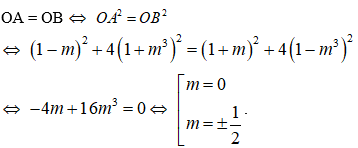
Đối chiếu với điều kiện (1), ta thấy chỉ thỏa mãn yêu cầu bài toán.
Câu 20:
Hàm số có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là:
 Xem đáp án
Xem đáp án
Chọn C.
![]()
![]()
![]()
![]()
Khi đó:
![]()
=> Hàm số có giá trị lớn nhất bằng 2, giá trị nhỏ nhất bằng
Câu 21:
Tập nghiệm của bất phương trình là
 Xem đáp án
Xem đáp án
Đặt t = 4x (t > 0), khi đó bất phương trình đã cho tương đương với

Chọn A
Câu 23:
Nghiệm nguyên nhỏ nhất của bất phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện: x > 2
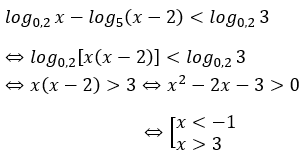
So điều kiện suy ra x > 3
Vậy nghiệm nguyên nhỏ nhất của bất phương trình đã cho là x = 4
Chọn A
Câu 24:
Nghiệm nguyên lớn nhất của bất phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện: x > 0
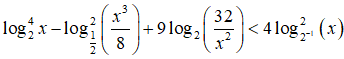
![]()
![]()
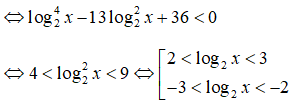
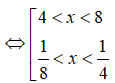
Suy ra, nghiệm nguyên lớn nhất của bất phương trình là x = 7.
Chọn A.
Câu 25:
Tích các nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện: x > 0
Ta có:
![]()

Vậy tập nghiệm của phương trình đã cho là
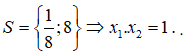
Chọn A