Giá trị của m để đồ thị hàm số không có tiệm cận đứng là
A. m = 0; m = ±1.
B. m = -1
C. m = ±1
D. m = 1
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Xét m = 0 thì đồ thị hàm số là đường thẳng y = -x là 1 đường thẳng nên không có đường tiệm cận đứng.
Xét m ≠ 0 khi đó đồ thị hàm số không có đường tiệm cận đứng nếu ![]()
(khi đó hàm số suy biến có đạo hàm y’ = 0)
Vậy giá trị của m cần tìm là m = 0; m = ±1.
Cho hàm số có đồ thị (C). Biết tiệm cận ngang của (C) đi qua điểm A(-1; 2) đồng thời điểm I(2; 1) thuộc (C). Khi đó giá trị của m + n là
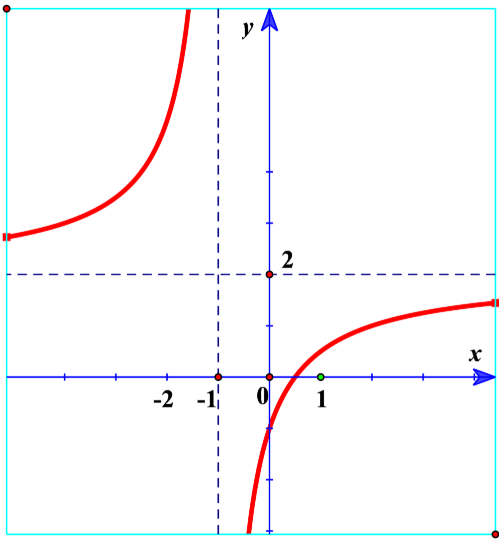
Cho đồ thị hàm số y = f(x) như hình bên. Khẳng định nào sau đây là đúng?
Tìm tất cả các giá trị thực của tham số m sao cho hàm số tăng trên từng khoảng xác định của nó?
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
Cho hàm số có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
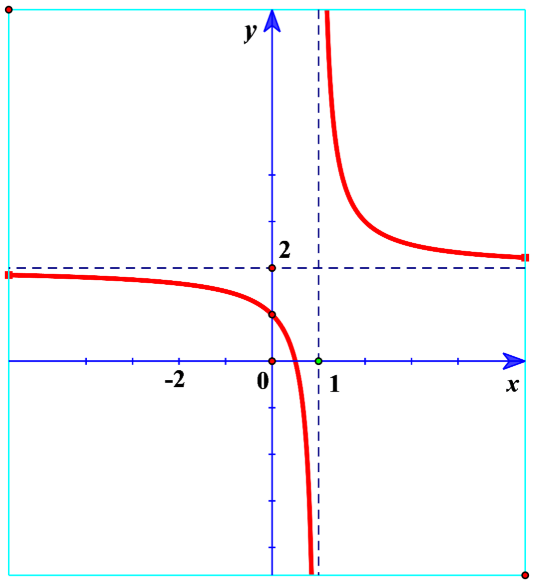
Xác định a, b, c để hàm số có đồ thị như hình vẽ bên. Chọn đáp án đúng?
Cho hàm số . Phương trình tiếp tuyến của (C) tại điểm M thuộc (C) và có hoành độ bằng 3
Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng (1; 3)?
Tập tất cả các giá trị của tham số m để đường thẳng cắt đồ thị hàm số tại ba điểm phân biệt là
Cho hàm số và các khoảng sau:
Hỏi hàm số đồng biến trên các khoảng nào?