Cho hình hộp ABCD.A'B'C'D'. Gọi I và K lần lượt là tâm của hình bình hành ABB’A’ và BCC’B’. Khẳng định nào sau đây sai?
A.
B. Bốn điểm I,K,C,A đồng phẳng
C.
D. Ba vecto không đồng phẳng
Giải bởi Vietjack
Đáp án D
+) A đúng do tính chất đường trung bình trong ΔB'AC và tính chất của hình bình hành ACC'A'.
+) B đúng do IK // AC nên bốn điểm I, K, C, A đồng phẳng.
+) C đúng do việc ta phân tích:
+) D sai do giá của ba vectơ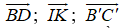 
đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
Trên đồ thị của hàm số có điểm M sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo thành một tam giác có diện tích bằng 2. Tìm tọa độ M?
Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
Phần I: Trắc nghiệm
Cho hình hộp ABCD.A'B'C'D' có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt . Khẳng định nào sau đây đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và Gọi M, N lần lượt là trung điểm của BC và CD: Chứng minh (SAC) ⊥ (SBD).
Cho hàm số g(x) = x.f(x) + x với f(x) là hàm số có đạo hàm trên R. Biết g'(3) = 2, f'(3) = -1 Giá trị của g(3) bằng:
Gọi S là tập các số nguyên của a sao cho có giá trị hữu hạn. Tính tổng các phần tử của S.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và(ABC).
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ tiếp điểm bằng 2 là:
Hãy viết số thập phân vô hạn tuần hoàn sau dưới dạng một phân số. α = 34,121212… (chu kỳ 12)
