Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
A. AC = BD
B. Δ ABD cân tại A.
C. BI là đường trung tuyến của Δ ABC
D. .
 Giải bởi Vietjack
Giải bởi Vietjack
Trong hình bình hành các góc đối bằng nhau
Hay 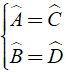
+ Δ ABD cân tại A khi và chỉ khi AB = AD nhưng theo giả thiết ta chưa có dữ kiện này
→ Đáp án B sai.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
→ Đáp án A sai vì theo giả thiết chưa đủ dữ kiện
+ Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên I là trung điểm của AC và BD nên BI là đường trung tuyến của Δ ABC
Chọn đáp án C.
Cho hình bình hành ABCD, gọi E và F là trung điểm của AD và BC. Gọi I là giao điểm của AC và BD. Tìm khẳng định sai?
Cho hình bình hành ABCD có , các góc còn lại của hình bình hành là?
Cho tam giác ABC có M, N và P lần lượt là trung điểm AB, AC và BC. Tìm khẳng định sai ?