Các giá trị của x để là ba số hạng liên tiếp của một cấp số cộng.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
- Để: là ba số hạng liên tiếp của một cấp số cộng thì:
- Biểu diễn 3 họ nghiệm đó trên đường tròn lượng giác thì vị trí các điểm xuất hiện là:
Do đó loại Đáp án B, C.
- Đáp án D. Thiếu nghiệm.
- Đáp án A. Đầy đủ nhất.
+) Với
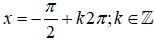
thì vị trí điểm biểu diễn là: -π/2 ứng với k = 0
+) Với
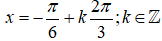
thì vị trí điểm biểu diễn là:
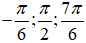
ứng với k = 0,1,2.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong các đẳng thức véc tơ sau đây, đẳng thức nào đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = x. Tìm x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc Biết SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh bên SA vuông góc với mặt đáy. Gọi H,K lần lượt là hình chiếu của A lên SC; SD. Dựng KN // CD, với N ∈ SC. Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hình chóp S.ABCD có SA ⊥ (ABCD), tứ giác ABCD là hình thang cân có đáy lớn AD gấp đôi đáy nhỏ BC và cạnh bên AB = BC. Mặt phẳng (P) đi qua A, vuông góc với SD và cắt SB, SC, SD lần lượt tại M, N, P. Khi đó ta có thể kết luận gì về tứ giác AMNP?
Cho hàm số f(x)liên tục trên đoạn [a ; b] và f(a) = b, f(b) = a, với 0 < a < b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b).
Cho dãy số xác định bởi và . Số hạng tổng quát của dãy số này là:
Cho tứ diện ABCD, biết hai tam giác ABC và BCD là hai tam giác cân có chung cạnh đáy BC. Gọi I là trung điểm của cạnh BC. Khẳng định nào đúng trong các khẳng định sau?
Một cấp số cộng gồm 8 số hạng với số hạng đầu bằng - 15 và số hạng cuối là 69. Tìm công sai của cấp số cộng.
Cho hàm số . Để tính đạo hàm f’(x), hai học sinh lập luận theo hai cách như sau:
- Hỏi cách nào đúng trong hai các giải trên?